题目内容
1.已知函数f(x)=sin(2x+$\frac{π}{3}$)与g(x)的图象关于直线x=$\frac{π}{6}$对称,将g(x)的图象向左平移φ(φ>0)个单位后与f(x)的图象重合,则φ的最小值为$\frac{π}{6}$.分析 由对称性可得函数g(x)的解析式,由图象平移和三角函数知识可得φ的方程,易得最小值.
解答 解:设P(x,y)为函数g(x)图象上的任意一点,
则P关于直线x=$\frac{π}{6}$的对称点P′($\frac{π}{3}$-x,y)在f(x)=sin(2x+$\frac{π}{3}$)图象上,
∴满足y=sin[2($\frac{π}{3}$-x)+$\frac{π}{3}$]=sin2x
其图象向左平移φ个单位后对应解析式y=sin(2x+2φ),
由图象和f(x)的图象重合可得$2φ=\frac{π}{3}+2kπ$,
即$φ=\frac{π}{6}+kπ(k∈N)$,∴${φ_{min}}=\frac{π}{6}$,
故答案为:$\frac{π}{6}$.
点评 本题考查三角函数的对称性以及函数图象的平移,属基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
9.设f0(x)=sinx,fn(x)=fn-1′(x),n∈N+,则f2010(x)=( )
| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
16.如图是秦九韶算法的一个程序框图,则输出的S为( )
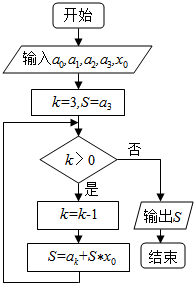

| A. | a1+x0(a3+x0(a0+a2x0))的值 | B. | a3+x0(a2+x0(a1+a0x0))的值 | ||
| C. | a0+x0(a1+x0(a2+a3x0))的值 | D. | a2+x0(a0+x0(a3+a1x0))的值 |
6.如图是一个几何体的三视图,则这个几何体的体积为( )
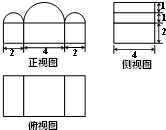

| A. | 16+3π | B. | 32+6π | C. | 64+12π | D. | 64+6π |
13.设a=sin42°,b=cos46°,c=2${\;}^{-\frac{1}{2}}$,则( )
| A. | c<a<b | B. | b<c<a | C. | a<b<c | D. | b<a<c |
10.已知向量$\overrightarrow a,\overrightarrow b$满足:$|\overrightarrow a|=13,|\overrightarrow b|=1,|\overrightarrow a-5\overrightarrow b|≤12$,则$\overrightarrow b$在$\overrightarrow a$上的投影长度的取值范围是( )
| A. | $[0,\frac{1}{13}]$ | B. | $[0,\frac{5}{13}]$ | C. | $[\frac{1}{13},1]$ | D. | $[\frac{5}{13},1]$ |
11.已知m,n是平面α外的两条不同的直线.若m,n在平面α内的射影分别是两条直线m′和n′,则“m⊥n”是“m′⊥n′”的( )
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
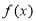 为奇函数,且当
为奇函数,且当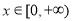 时,
时,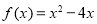 ,则
,则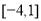 上的最大值为( )
上的最大值为( )