题目内容
9.设f0(x)=sinx,fn(x)=fn-1′(x),n∈N+,则f2010(x)=( )| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
分析 根据题意和求导公式依次求函数的导数,归纳出规律:周期性,即可求出f2010(x).
解答 解:由题意得,f0(x)=sinx,fn(x)=fn-1′(x),n∈N+,
则f1(x)=f0′(x)=cosx,f2(x)=f1′(x)=-sinx,
f3(x)=f2′(x)=-cosx,f4(x)=f3′(x)=sinx,…,
所以导函数具有周期性,且周期是4,
则f2010(x)=f2(x)=-sinx,
故选:B.
点评 本题考查导数的运算,以及周期性的应用,属于基础题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
14.设变量x,y满足约束条件$\left\{\begin{array}{l}{2x-y-7≥0}\\{x+y-8≥0}\\{x-2y-2≤0}\end{array}\right.$,则目标函数z=x2+y2的最小值为( )
| A. | 32 | B. | 17 | C. | 40 | D. | 34 |
19.某设备的使用年限x(单位:年)与所支付的维修费用y(单位:千元)的一组数据如表:
从散点图分析.y与x线性相关,根据上表中数据可得其线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的$\widehat{b}$=1.54.由此预测该设备的使用年限为6年时需支付的维修费用约是( )
| 使用年限x | 2 | 3 | 4 | 5 |
| 维修费用y | 2 | 3.4 | 5 | 6.6 |
| A. | 7.2千元 | B. | 7.8千元 | C. | 8.1千元 | D. | 9.5千元 |

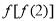 并判断函数
并判断函数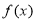 的奇偶性;
的奇偶性;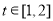 ,
,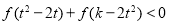 恒成立,求实数
恒成立,求实数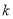 的取值范围.
的取值范围.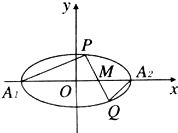 若双曲线$\frac{{x}^{2}}{8}$-y2=1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且它们的离心率互为倒数.
若双曲线$\frac{{x}^{2}}{8}$-y2=1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且它们的离心率互为倒数.