题目内容
椭圆的中心是原点O,它的短轴长为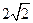 ,相应于焦点F(c,0)(c>0)的准线
,相应于焦点F(c,0)(c>0)的准线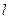 与x轴相交于点A,
与x轴相交于点A,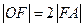 ,过点A的直线与椭圆相交于P,Q两点,
,过点A的直线与椭圆相交于P,Q两点,
(1)求椭圆的离心率及方程。
(2)若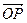 ·
·
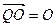 ,求直线PQ的方
,求直线PQ的方 程。
程。
(3)设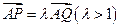 ,过点P且平行于准线l的直线与椭圆相交于另一点M,证明
,过点P且平行于准线l的直线与椭圆相交于另一点M,证明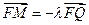
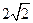 ,相应于焦点F(c,0)(c>0)的准线
,相应于焦点F(c,0)(c>0)的准线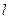 与x轴相交于点A,
与x轴相交于点A,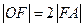 ,过点A的直线与椭圆相交于P,Q两点,
,过点A的直线与椭圆相交于P,Q两点,(1)求椭圆的离心率及方程。
(2)若
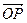 ·
·
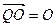 ,求直线PQ的方
,求直线PQ的方 程。
程。(3)设
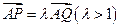 ,过点P且平行于准线l的直线与椭圆相交于另一点M,证明
,过点P且平行于准线l的直线与椭圆相交于另一点M,证明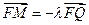

略

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 的左右焦点为
的左右焦点为 ,抛物线C:
,抛物线C: 以F2为焦点且与椭圆相交于点M
以F2为焦点且与椭圆相交于点M 、N
、N ,直线
,直线 与抛物线C相切
与抛物线C相切 本小题满分12分)
本小题满分12分)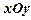 中,椭圆
中,椭圆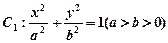 的左、右焦点分别为
的左、右焦点分别为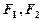 . 其中
. 其中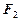 也是抛物线
也是抛物线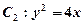 的焦点,点
的焦点,点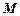 为
为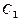 与
与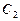 在第一象限的交点,且
在第一象限的交点,且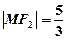
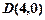 的直线
的直线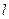 与
与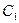 交于不同的两点
交于不同的两点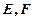 .
.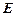 在
在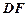 之间,试求
之间,试求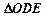 与
与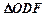 面积之比的取值范围.(O为坐标原点)
面积之比的取值范围.(O为坐标原点)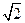 、离心率为
、离心率为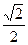 ,直线
,直线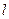 与y轴交于点P(0,
与y轴交于点P(0,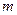 ),与
),与 椭圆C交于相异两点A、B,且
椭圆C交于相异两点A、B,且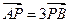 。
。 (F
(F



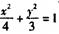 的右焦点F为圆心,并过椭圆的短轴端点的圆的方程为_
的右焦点F为圆心,并过椭圆的短轴端点的圆的方程为_ ,双曲线
,双曲线 ,抛物线
,抛物线 (其中
(其中 的离心率分别为
的离心率分别为 ,则
,则
 的值为 ( )
的值为 ( ) 





 与
与 有关
有关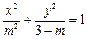 的一个焦点为
的一个焦点为 ,则
,则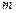 等于 .
等于 .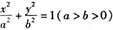 的左、右焦点分别为F1 F2,以F1 F2为直径的圆与椭圆在y轴左侧的部分交于A,B两点,且ΔF2AB是等边三角形,则椭圆的离心率为______
的左、右焦点分别为F1 F2,以F1 F2为直径的圆与椭圆在y轴左侧的部分交于A,B两点,且ΔF2AB是等边三角形,则椭圆的离心率为______