题目内容
、设椭圆 ,双曲线
,双曲线 ,抛物线
,抛物线 (其中
(其中 的离心率分别为
的离心率分别为 ,则
,则
 的值为 ( )
的值为 ( )






 与
与 有关
有关
 ,双曲线
,双曲线 ,抛物线
,抛物线 (其中
(其中 的离心率分别为
的离心率分别为 ,则
,则
 的值为 ( )
的值为 ( ) 





 与
与 有关
有关C
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
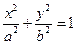 (a>b>0)的离心率
(a>b>0)的离心率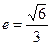 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为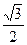 .
.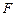 是椭圆
是椭圆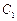 :
: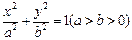 的右焦点,也是抛物线
的右焦点,也是抛物线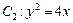 的焦点,点P为
的焦点,点P为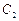 在第一象限的交点,且
在第一象限的交点,且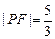 .
.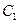 的方程;
的方程;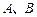 ,过
,过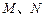 两点,记
两点,记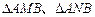 的面积分别为
的面积分别为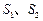 ,求
,求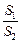 的取值范围。
的取值范围。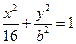
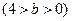 ,
,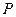 为椭圆上的动点,
为椭圆上的动点,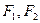 为椭圆的两焦点,当
为椭圆的两焦点,当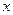 轴上时,过
轴上时,过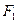 作
作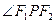 的外角平分线的垂线
的外角平分线的垂线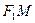 ,垂足为
,垂足为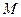 ,当点
,当点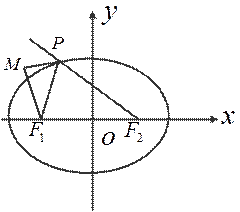
 的方程;
的方程; 、
、 ,试探究是否存在这样的点
,试探究是否存在这样的点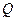 :点
:点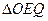 的面积
的面积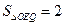 ?若存
?若存 在,求出点
在,求出点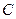 :
: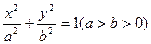 ,
,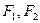 分别为左,右焦点,离心率为
分别为左,右焦点,离心率为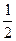 ,点
,点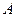 在椭圆
在椭圆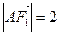 ,
,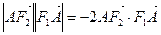 ,过
,过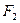 与坐标轴不垂直的直线
与坐标轴不垂直的直线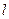 交椭圆于
交椭圆于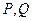 两点.
两点.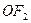 上是否存在点
上是否存在点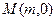 ,使得以线段
,使得以线段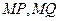 为邻边的四边形是菱形?若存在,求出实数
为邻边的四边形是菱形?若存在,求出实数 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.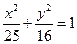 的顶点为焦点,焦点为顶点的双曲线方程,并求出其离心率.
的顶点为焦点,焦点为顶点的双曲线方程,并求出其离心率.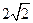 ,相应于焦点F(c,0)(c>0)的准线
,相应于焦点F(c,0)(c>0)的准线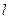 与x轴相交于点A,
与x轴相交于点A,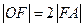 ,过点A的直线与椭圆相交于P,Q两点,
,过点A的直线与椭圆相交于P,Q两点,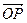 ·
·
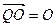 ,求直线PQ的方
,求直线PQ的方 程。
程。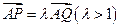 ,过点P且平行于准线l的直线与椭圆相交于另一点M,证明
,过点P且平行于准线l的直线与椭圆相交于另一点M,证明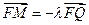

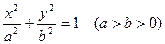 ,
,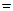 90°,求椭圆的离心率;
90°,求椭圆的离心率;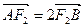 ,
,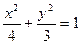 的长轴两端点为
的长轴两端点为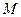 、
、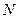 ,异于
,异于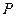 在椭圆上,则
在椭圆上,则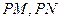 的斜率之积为 .
的斜率之积为 .