题目内容
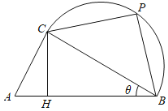
【题目】如图，正方体
的棱长为4，点E、F为棱CD、
的中点.
（1）求证：
平面
；
（2）求直线
与平面ACF所成角的正弦值.
【答案】（1）证明见详解；（2）
【解析】
（1）取
的中点
，连接
、
，易证四边形
是平行四边形，从而证得
，则根据线面平行的判定定理即可证明
平面
；
（2）以点
为坐标原点，分别以
、
、
所在直线为
、
、
轴，建立空间直角坐标系.求出平面
的一个法向量，和
，利用空间向量法，即可求线
与平面所成角的正弦值.
解：（1）证明：取的中点，连接、，
易知
，且，
四边形是平行四边形，
，
又
平面，
平面，
平面；
（2）如图所示，以点为坐标原点，分别以、、
所在直线为、、轴，建立空间直角坐标系，
则
，
，
，
，
，
，
，
，
设
为平面的一个法向量，
则
，即
令
，得
，
故：与平面所成角的正弦值为.
激活思维优加课堂系列答案
活力试卷系列答案
【题目】某连锁餐厅新店开业，打算举办一次食品交易会，招待新老顾客试吃.项目经理通过查阅最近
次食品交易会参会人数
（万人）与餐厅所用原材料数量
（袋），得到如下统计表：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数（万人） |
|
|
|
|
|
原材料（袋） |
|
|
|
|
|
（1）根据所给组数据，求出关于的线性回归方程
；
（2）已知购买原材料的费用
（元）与数量
（袋）的关系为
，投入使用的每袋原材料相应的销售收入为
元，多余的原材料只能无偿返还，据悉本次交易大会大约有
万人参加，根据（1）中求出的线性回归方程，预测餐厅应购买多少袋原材料，才能获得最大利润，最大利润是多少？（注：利润
销售收入
原材料费用）.
参考公式：
，
.
参考数据：
，
，
.
【题目】第7届世界军人运动会于2019年10月18日至27日在湖北武汉举行，赛期10天，共设置射击、游泳、田径、篮球等27个大项，329个小项，共有来自100多个国家的近万名现役军人同台竞技．前期为迎接军运会顺利召开，特招聘了3万名志愿者．某部门为了了解志愿者的基本情况，调查了其中100名志愿者的年龄，得到了他们年龄的中位数为34岁，年龄在
岁内的人数为15人，并根据调查结果画出如所示的频率分布直方图：
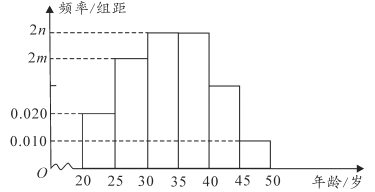
（1）求
，
的值并估算出志愿者的平均年龄（同一组的数据用该组区间的中点值代表）；
（2）本次军运会志愿者主要通过直接到武汉军运会执委会志愿者部现场报名和登录第七届世界军运会官网报名，即现场和网络两种方式报名调查．这100位志愿者的报名方式部分数据如下表所示，完善下面的表格，通过计算说明能否在犯错误的概率不超过0.001的前提下，认为“选择哪种报名方式与性别有关系”？
男性 | 女性 | 总计 | |
现场报名 | 50 | ||
网络报名 | 31 | ||
总计 | 50 |
参考公式及数据：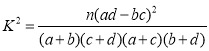
，其中
.
| 0.05 | 0.01 | 0.005 | 0.001 |
3.841 | 6.635 | 7.879 | 10.828 |
