题目内容
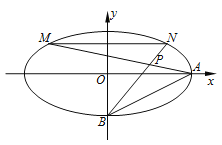
【题目】如图,点![]() 在以
在以![]() 为直径的圆
为直径的圆![]() 上,
上,![]() 垂直与圆
垂直与圆![]() 所在平面,
所在平面,![]() 为
为![]() 的垂心.
的垂心.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)延长![]() 交
交![]() 于点
于点![]() ,由重心性质及中位线性质可得
,由重心性质及中位线性质可得![]() ,再结合圆的性质得
,再结合圆的性质得![]() ,由已知
,由已知![]() ,可证
,可证![]() 平面
平面![]() ,进一步可得平面
,进一步可得平面![]() 平面
平面![]() (2)以点
(2)以点![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 方向分别为
方向分别为![]() ,
, ![]() ,
, ![]() 轴正方向建立空间直角坐标系,写出各点坐标,利用二面角与二个半平面的法向量的夹角间的关系可求二面角的余弦值.
轴正方向建立空间直角坐标系,写出各点坐标,利用二面角与二个半平面的法向量的夹角间的关系可求二面角的余弦值.
试题解析:(1)如图,延长![]() 交
交![]() 于点
于点![]() .因为
.因为![]() 为
为![]() 的重心,所以
的重心,所以![]() 为
为![]() 的中点.
的中点.
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() .因为
.因为![]() 是圆
是圆![]() 的直径,所以
的直径,所以![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .又
.又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() =
= ![]() ,所以
,所以![]() 平面
平面![]() .即
.即![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以平面
,所以平面![]()
![]() 平面
平面![]() .
.
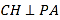
(2)以点![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 方向分别为
方向分别为![]() ,
, ![]() ,
, ![]() 轴正方向建立空间直角坐标系
轴正方向建立空间直角坐标系![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, 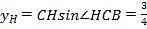 ,
, ![]() ,
, ![]() ,则
,则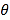 ,
, 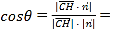 .平面
.平面![]() 即为平面
即为平面![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则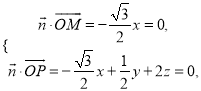 令
令![]() ,得
,得![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,由
,由![]() 平面
平面![]() ,易得
,易得![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,即
,即![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
在![]() 中,由
中,由![]() ,得
,得![]() ,则
,则![]() ,
, ![]() .
.
所以![]() ,
, ![]() .所以
.所以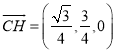 .
.
设二面角![]() 的大小为
的大小为![]() ,则
,则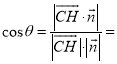
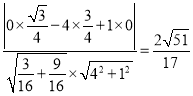 .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目