题目内容
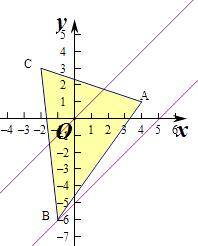
【题目】已知D是以点A（4，1），B（﹣1，﹣6），C（﹣2，3）为顶点的三角形区域（包括边界及内部）．
（1）写出表示区域D的不等式组；
（2）设点B（﹣1，﹣6）、C（﹣2，3）在直线4x﹣3y﹣a=0的异侧，求a的取值范围；
（3）若目标函数z=kx+y（k＜0）的最小值为﹣k﹣6，求k的取值范围．
【答案】
（1）解：A（4，1），B（﹣1，﹣6），C（﹣2，3）为顶点，
则直线方程AB： 
得7x﹣5y﹣23=0，
AC： 
，即x+3y﹣7=0，
BC： 
，即9x+y+15=0，
则对应的不等式组为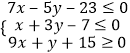 
（2）解：∵点B（﹣1，﹣6）、C（﹣2，3）在直线4x﹣3y﹣a=0的异侧，
∴将点的坐标分别代入得（14﹣a）（﹣17﹣a）＜0，
即（a﹣14）（a+17）＜0，得﹣17＜a＜14
（3）∵z=kx+y（k＜0）的最小值为﹣k﹣6，这也是将点B（﹣1，﹣6）的坐标代入的结果，
∴B是目标函数的最优解，
∵y=﹣kx+z，∴0＜﹣k＜kAB或kBC＜﹣k＜0，（∵k＜0，∴这种情况不存在）
∵kAB= 
，∴0＜﹣k＜ ，即﹣ ＜k＜0
【解析】（1）先分别求出AB，BC，AB的方程，结合二元一次不等式组表示平面区域进行表示，（2）根据点与直线的位置关系转化为二元一次不等式关系进行求解即可．（3）根据线性规划的知识建立直线斜率关系进行求解即可．
练习册系列答案
备战中考寒假系列答案
相关题目
