题目内容
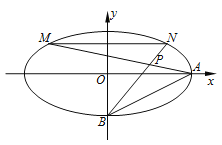
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 过点
过点![]() ,
, ![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的右、下顶点,且
的右、下顶点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 在椭圆
在椭圆![]() 内,满足直线
内,满足直线![]() ,
, ![]() 的斜率乘积为
的斜率乘积为![]() ,且直线
,且直线![]() ,
, ![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() ,
, ![]() .
.
(i) 若![]() ,
, ![]() 关于
关于![]() 轴对称,求直线
轴对称,求直线![]() 的斜率;
的斜率;
(ii) 求证: ![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.
【答案】(1)![]() . (2)(i)
. (2)(i) ![]() ;(ii) 见解析.
;(ii) 见解析.
【解析】试题分析:
(1)由题意求得![]() ,椭圆的方程为
,椭圆的方程为![]() .
.
(2)(i)设出点的坐标和直线方程,联立直线与椭圆的方程,得到关于实数k的方程,解方程可得![]() ;
;
(ii)利用题意证得![]() ,则
,则![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.
试题解析:
(1)由![]() 知,
知, ![]() ,
,
又椭圆![]() 过点
过点![]() ,所以
,所以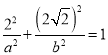 ,
,
解得![]() 所以椭圆
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
联立![]() 消去
消去![]() 并整理得,
并整理得, ![]() ,
,
解得![]() ,
, ![]() ,所以
,所以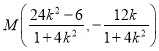 .
.
因为直线![]() ,
, ![]() 的斜率乘积为
的斜率乘积为![]() ,所以直线
,所以直线![]() 的方程
的方程![]() .
.
联立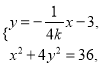 消去
消去![]() 并整理得,
并整理得, ![]() ,
,
解得![]() ,
, ![]() ,所以
,所以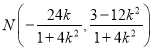 .
.
(i) 因为![]() ,
, ![]() 关于
关于![]() 轴对称,所以
轴对称,所以![]() ,
,
即![]() ,解得
,解得![]() .
.
当![]() 时,点
时,点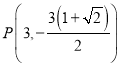 在椭圆
在椭圆![]() 外,不满足题意.
外,不满足题意.
所以直线![]() 的斜率为
的斜率为![]() .
.
(ii) 联立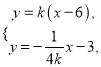 解得
解得![]() .
.
所以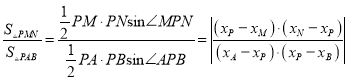
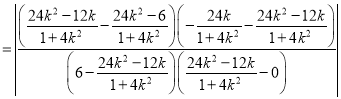
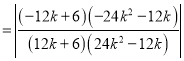
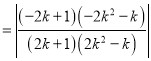
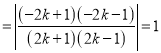 .
.
故![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
【题目】本市某玩具生产公司根据市场调查分析,决定调整产品生产方案,准备每天生产![]() ,
, ![]() ,
, ![]() 三种玩具共100个,且
三种玩具共100个,且![]() 种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
玩具名称 |
|
|
|
工时(分钟) | 5 | 7 | 4 |
利润(元) | 5 | 6 | 3 |
(Ⅰ)用每天生产![]() 种玩具个数
种玩具个数![]() 与
与![]() 种玩具
种玩具![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(Ⅱ)怎样分配生产任务才能使每天的利润最大,最大利润是多少?