题目内容
已知奇函数f(x)在[a,b]上是减函数,试判断它在[-b,-a]的单调性,并加以证明。
见解析
解:奇函数f(x)在[-b,-a]上也是减函数。证明如下:
设-b<x1<x2<-a,则a<-x2<-x1<b.因为f(x)在[a,b](0<a<b)上是减函数,所以
f(-x2)>f(-x1),又因为f(x)是奇函数,所以
f(-x)=-f(x),于是-f(x2)>-f(x1) ,即
f(x1)>f(x2),所以f(x)在[-b,-a]上是减函数
设-b<x1<x2<-a,则a<-x2<-x1<b.因为f(x)在[a,b](0<a<b)上是减函数,所以
f(-x2)>f(-x1),又因为f(x)是奇函数,所以
f(-x)=-f(x),于是-f(x2)>-f(x1) ,即
f(x1)>f(x2),所以f(x)在[-b,-a]上是减函数

练习册系列答案
相关题目
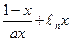 在[1,+∞
在[1,+∞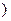 上为增函数.
上为增函数.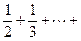
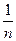
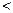
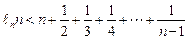 (n∈N*且n ≥ 2 )
(n∈N*且n ≥ 2 )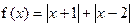 。
。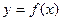 的图像;
的图像;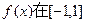 上是增函数,且
上是增函数,且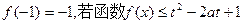 对所有的
对所有的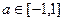 ,
,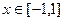 都成立,则t的取值范围是________________
都成立,则t的取值范围是________________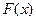 和
和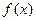 都在区间
都在区间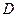 上有定义,若对
上有定义,若对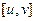 ,总有
,总有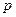 和
和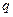 ,使得不等式
,使得不等式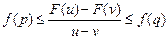 成立,则称
成立,则称 在区间
在区间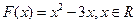 ,那么
,那么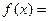 _____________
_____________ 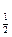 (3x
(3x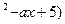 在[-1,+∞)上是减函数,则实数a的取值范围( )
在[-1,+∞)上是减函数,则实数a的取值范围( )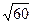 <a<-6 C -8<a≤-6 D
<a<-6 C -8<a≤-6 D  -8≤a≤-6
-8≤a≤-6 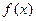 在区间
在区间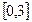 上的图象如图所示,即
上的图象如图所示,即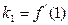 ,
,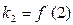 ,
,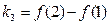 ,则
,则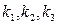 之间的大小关系为( )
之间的大小关系为( )




 的单调递减区间是__________.
的单调递减区间是__________.