题目内容
(本小题满分12分)
若函数f(x)=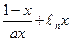 在[1,+∞
在[1,+∞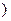 上为增函数.
上为增函数.
(Ⅰ)求正实数a的取值范围.
(Ⅱ)若a=1,求征: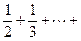
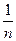
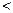
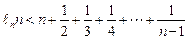 (n∈N*且n ≥ 2 )
(n∈N*且n ≥ 2 )
若函数f(x)=
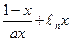 在[1,+∞
在[1,+∞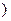 上为增函数.
上为增函数.(Ⅰ)求正实数a的取值范围.
(Ⅱ)若a=1,求征:
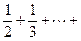
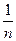
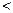
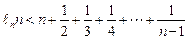 (n∈N*且n ≥ 2 )
(n∈N*且n ≥ 2 )(Ⅰ)a≥1
(Ⅱ)证明见解析
(Ⅱ)证明见解析
(Ⅰ)由已知: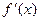 =
=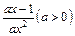
依题意得: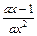 ≥0对x∈[1,+∞
≥0对x∈[1,+∞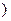 恒成立
恒成立
∴ax-1≥0对x∈[1,+∞ 恒成立
恒成立
∴a-1≥0即:a≥1
(Ⅱ)∵a="1 " ∴由(1)知:f(x)=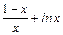 在[1,+∞
在[1,+∞ 上为增函数,
上为增函数,
∴n≥2时:f(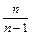 )=
)=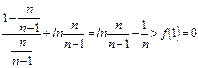
即: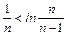
∴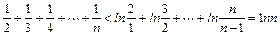
设g(x)=lnx-x x∈[1,+∞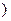 ,
,
则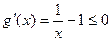 对
对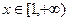 恒成立,
恒成立,
∴g′(x)在[1+∞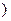 为
为 减函数…
减函数…
∴n≥2时:g(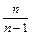 )=ln
)=ln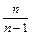 -
-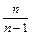 <g(1)=-1<0
<g(1)=-1<0
即:ln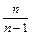 <
<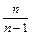 =1+
=1+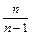 (n≥2)
(n≥2)
∴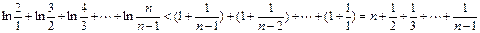
综上所证: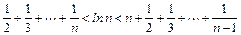 (n∈N*且≥2)成立.
(n∈N*且≥2)成立.
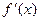 =
=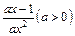
依题意得:
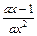 ≥0对x∈[1,+∞
≥0对x∈[1,+∞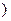 恒成立
恒成立∴ax-1≥0对x∈[1,+∞
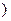 恒成立
恒成立∴a-1≥0即:a≥1
(Ⅱ)∵a="1 " ∴由(1)知:f(x)=
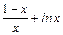 在[1,+∞
在[1,+∞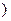 上为增函数,
上为增函数,∴n≥2时:f(
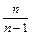 )=
)=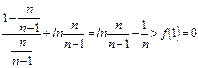
即:
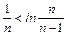
∴
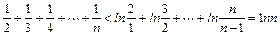
设g(x)=lnx-x x∈[1,+∞
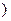 ,
,则
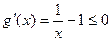 对
对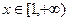 恒成立,
恒成立,∴g′(x)在[1+∞
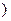 为
为 减函数…
减函数…∴n≥2时:g(
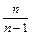 )=ln
)=ln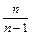 -
-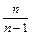 <g(1)=-1<0
<g(1)=-1<0即:ln
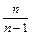 <
<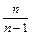 =1+
=1+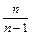 (n≥2)
(n≥2)∴
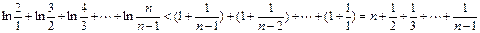
综上所证:
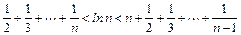 (n∈N*且≥2)成立.
(n∈N*且≥2)成立.
练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
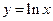 关于直线
关于直线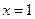 对称的函数为
对称的函数为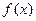 ,又函数
,又函数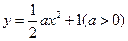 的导函数为
的导函数为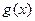 ,记
,记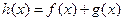 .
.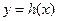 在点
在点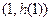 处的切线为
处的切线为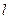 ,
, 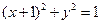 相切,求
相切,求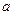 的值;
的值;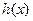 的单调区间;
的单调区间;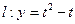 (
(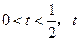 为常数)与函数
为常数)与函数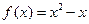 的图象以及y轴所围成的封闭图形的面积为
的图象以及y轴所围成的封闭图形的面积为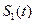 ,若直线l与函数
,若直线l与函数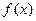 的图象所围成的封闭图形的面积为
的图象所围成的封闭图形的面积为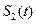 ,已知
,已知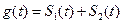 ,当
,当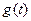 取最小值时,求t的值.
取最小值时,求t的值.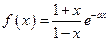 。
。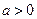 ,讨论
,讨论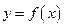 的单调性;
的单调性;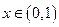 恒有
恒有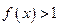 ,求
,求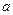 的取值范围。
的取值范围。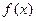 对任意
对任意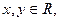 ,都有
,都有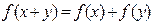 ,
,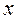 > 0时,
> 0时,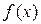 < 0,
< 0,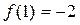 .
. 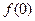 ;
; 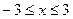 时,
时,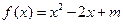 在
在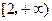 的最小值为-2,则实数
的最小值为-2,则实数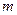 的值为( )
的值为( )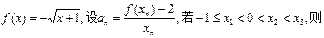
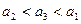
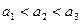
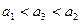
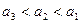
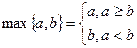 ,设实数
,设实数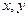 满足约束条件
满足约束条件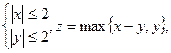 则
则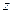 的取值范围是( )。
的取值范围是( )。