题目内容
若地球半径为R,在北纬45°圈上有A、B两点,且这两点间的球面距离为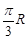 ,则北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的余弦值为 ( )
,则北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的余弦值为 ( )
(A)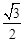 (B)
(B)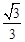 (C)
(C)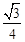 (D)
(D)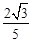
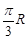 ,则北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的余弦值为 ( )
,则北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的余弦值为 ( ) (A)
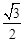 (B)
(B)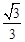 (C)
(C)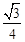 (D)
(D)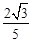
B
A、B两点间的球面距离为以O为圆心,且过A,B的圆中弧AB的长度,
设∠AOB=α,则α•R=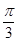 R,α=
R,α=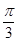 ,又OA=OB,∴△AOB为正三角形,∴AB=R.
,又OA=OB,∴△AOB为正三角形,∴AB=R.
设Q为北纬45°圈的圆心,则由球的截面圆形状可知,OQ⊥⊙Q面,∠OAQ=45°,
且截面圆半径长QA=R•cos∠OAQ=R•cos45°=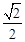 R.在△QAB中,
R.在△QAB中, 得△QAB为等腰直角三角形.设M为AB中点,连接QM,OM,则OM⊥AB,QM⊥AB,
得△QAB为等腰直角三角形.设M为AB中点,连接QM,OM,则OM⊥AB,QM⊥AB,
∴∠OMQ为北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的平面角.
在RT△OMQ中,cos∠OMQ=QM/OM ="="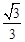 ,所以所求二面角的余弦值是
,所以所求二面角的余弦值是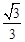 ,故选B.
,故选B.
设∠AOB=α,则α•R=
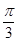 R,α=
R,α=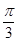 ,又OA=OB,∴△AOB为正三角形,∴AB=R.
,又OA=OB,∴△AOB为正三角形,∴AB=R.设Q为北纬45°圈的圆心,则由球的截面圆形状可知,OQ⊥⊙Q面,∠OAQ=45°,
且截面圆半径长QA=R•cos∠OAQ=R•cos45°=
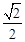 R.在△QAB中,
R.在△QAB中, 得△QAB为等腰直角三角形.设M为AB中点,连接QM,OM,则OM⊥AB,QM⊥AB,
得△QAB为等腰直角三角形.设M为AB中点,连接QM,OM,则OM⊥AB,QM⊥AB,∴∠OMQ为北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的平面角.
在RT△OMQ中,cos∠OMQ=QM/OM ="="
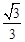 ,所以所求二面角的余弦值是
,所以所求二面角的余弦值是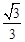 ,故选B.
,故选B.
练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
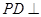 平面
平面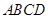 ,
,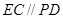 ,且
,且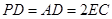 ="2" .
="2" .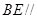 平面
平面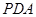 ;
;
 π
π π
π  π
π π
π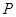 在圆柱
在圆柱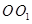 的底面圆
的底面圆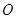 上,
上,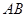 为圆
为圆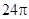 ,
,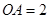 ,
,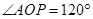 。
。 的体积。
的体积。 与
与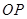 所成角的余弦值;
所成角的余弦值;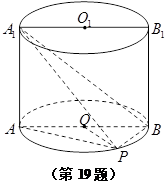
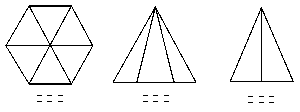
 是边长为2的正三角形,俯视图为正六边形,那么该几何体的体积为( )
是边长为2的正三角形,俯视图为正六边形,那么该几何体的体积为( )
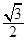
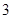
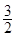
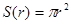 ,周长
,周长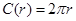 ,若将
,若将 看作是
看作是 上的变量,则
上的变量,则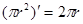 ……①,这里①式可以用语言表达为:圆的面积函数的导数等于圆的周长函数.对于半径为
……①,这里①式可以用语言表达为:圆的面积函数的导数等于圆的周长函数.对于半径为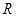 的球,若将
的球,若将 中,
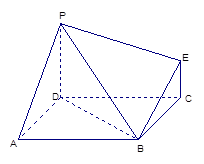
中, 为正方形且边长为
为正方形且边长为 ,面
,面 面
面 ,
,  ,
, ,
, ,则该组合体的体积为( )
,则该组合体的体积为( )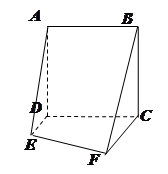



 的内切圆面积为
的内切圆面积为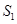 ,外接圆面积为
,外接圆面积为 ,则
,则 ,推广到空间几何中可以得到类似结论:若正四面体
,推广到空间几何中可以得到类似结论:若正四面体 的内切球体积为
的内切球体积为 ,外接球体积为
,外接球体积为 ,则
,则 ( )
( )

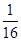

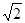 ,
,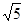 ,
,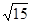 ,试求它的外接球的表面积和体积。
,试求它的外接球的表面积和体积。