题目内容
(本小题满分14分)
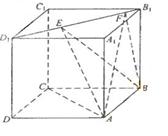
右图为一简单组合体,其底面ABCD为正方形,
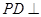 平面
平面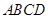 ,
,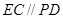 ,且
,且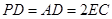 ="2" .
="2" .
(1)求证: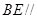 平面
平面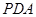 ;
;
(2)求四棱锥B-CEPD的体积.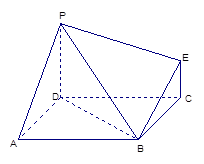
右图为一简单组合体,其底面ABCD为正方形,
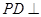 平面
平面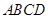 ,
,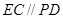 ,且
,且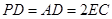 ="2" .
="2" .(1)求证:
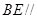 平面
平面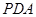 ;
;(2)求四棱锥B-CEPD的体积.

(1)见解析;(2)2.
(1)取PD的中点F,证明四边形AFEB为平行四边形即可.
(2)根据体积公式求出四边形PDCE的面积,高BC的长即可.
证明:法1:取PD的中点F,连接EF、AF,则 …………1分
…………1分
∴四边形EFDC是平行四边形,
∵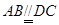 ∴
∴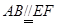 …………3分
…………3分
∴四边形EFAB是平行四边形 ∴ …………4分
…………4分
∵ ,
, ∴
∴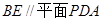 …………6分
…………6分
法2:∵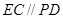 ,
,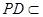 平面
平面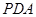 ,
,
 平面
平面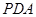
∴EC//平面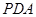 , …………2分
, …………2分
同理可得BC//平面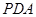 …………3分
…………3分
∵EC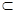 平面EBC,BC
平面EBC,BC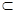 平面EBC且
平面EBC且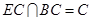
∴平面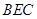 //平面
//平面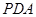 …………5分
…………5分
又∵BE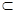 平面EBC ∴BE//平面PDA …………6分
平面EBC ∴BE//平面PDA …………6分
(2)∵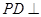 平面
平面 ,
,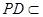 平面
平面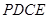
∴平面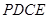
 平面ABCD …………8分
平面ABCD …………8分
∵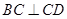 ∴BC
∴BC 平面
平面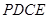 …………10分
…………10分
∵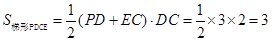 …………12分
…………12分
∴四棱锥B-CEPD的体积
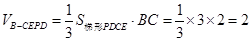 . …………14分
. …………14分
(2)根据体积公式求出四边形PDCE的面积,高BC的长即可.
证明:法1:取PD的中点F,连接EF、AF,则
 …………1分
…………1分 ∴四边形EFDC是平行四边形,

∵
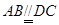 ∴
∴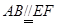 …………3分
…………3分 ∴四边形EFAB是平行四边形 ∴
 …………4分
…………4分∵
 ,
, ∴
∴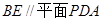 …………6分
…………6分法2:∵
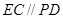 ,
,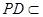 平面
平面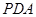 ,
, 平面
平面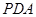
∴EC//平面
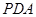 , …………2分
, …………2分 同理可得BC//平面
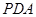 …………3分
…………3分 ∵EC
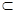 平面EBC,BC
平面EBC,BC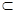 平面EBC且
平面EBC且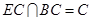
∴平面
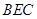 //平面
//平面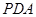 …………5分
…………5分 又∵BE
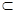 平面EBC ∴BE//平面PDA …………6分
平面EBC ∴BE//平面PDA …………6分 (2)∵
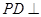 平面
平面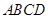 ,
,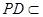 平面
平面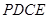
∴平面
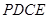
 平面ABCD …………8分
平面ABCD …………8分 ∵
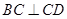 ∴BC
∴BC 平面
平面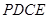 …………10分
…………10分 ∵
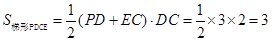 …………12分
…………12分 ∴四棱锥B-CEPD的体积
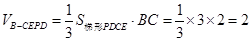 . …………14分
. …………14分
练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 中,
中, ,
, ,点
,点 ,
, 分别是
分别是 ,
, 的中点.
的中点.
 ⊥平面
⊥平面 ;
; ⊥平面
⊥平面 ,求三棱锥
,求三棱锥 的体积.
的体积. ,一侧棱到对面的距离不小于
,一侧棱到对面的距离不小于 ,从此三棱柱中去掉以此侧棱为直径的球所占的部分,余下的几何体的表面积与原三棱柱的表面积相等,则所剩几何体的体积最小值为 .
,从此三棱柱中去掉以此侧棱为直径的球所占的部分,余下的几何体的表面积与原三棱柱的表面积相等,则所剩几何体的体积最小值为 . 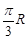 ,则北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的余弦值为 ( )
,则北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的余弦值为 ( ) 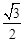 (B)
(B)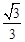 (C)
(C)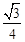 (D)
(D)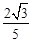
 .(用数值作答)
.(用数值作答)
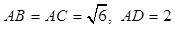 ,则AD两点间的球面距离
,则AD两点间的球面距离 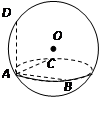
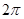 ,底面面积为
,底面面积为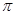 ,则该圆锥的体积为 。
,则该圆锥的体积为 。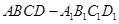 的棱长为1,线段
的棱长为1,线段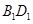 上有两个动点E, F,且
上有两个动点E, F,且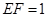 ,则四面体
,则四面体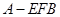 的体积
的体积