题目内容
已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )
A.5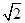 -4 -4 | B.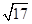 -1 -1 | C.6-2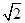 | D.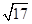 |
A
解析试题分析:圆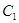 关于
关于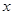 轴对称圆的圆心坐标
轴对称圆的圆心坐标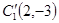 ,半径不变,圆
,半径不变,圆 的圆心坐标
的圆心坐标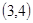 半径
半径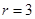
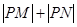 的最小值为连接圆
的最小值为连接圆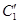 与圆
与圆 圆心,再减去两圆的半径因此
圆心,再减去两圆的半径因此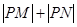 的最小值
的最小值
考点:圆与圆的位置关系.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
设双曲线  ,离心率
,离心率  ,右焦点
,右焦点  ,方程
,方程  的两个实数根分别为
的两个实数根分别为  ,则点
,则点  与圆
与圆  的位置关系
的位置关系
| A.在圆内 | B.在圆上 | C.在圆外 | D.不确定 |
动圆 经过点
经过点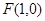 并且与直线
并且与直线 相切,若动圆
相切,若动圆 与直线
与直线 总有公共点,则圆
总有公共点,则圆 的面积( )
的面积( )
A.有最大值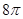 | B.有最小值 | C.有最小值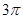 | D.有最小值 |
过点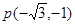 的直线l与圆
的直线l与圆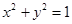 有公共点,则直线l的倾斜角的取值范围是
有公共点,则直线l的倾斜角的取值范围是
A.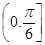 | B.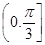 | C.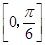  | D.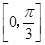 |
当曲线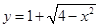
 与直线
与直线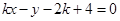 有两个相异的交点时,实数k的取值范围是( )
有两个相异的交点时,实数k的取值范围是( )
A.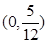 | B.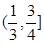 | C.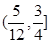 | D.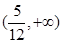 |
过点A(-1,0),斜率为k的直线,被圆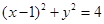 截得的弦长为2
截得的弦长为2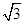 ,则k的值为( )。
,则k的值为( )。
A.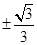 | B. | C.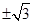 | D.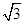 |
已知直线l过点(-2,0),当直线l与圆x2+y2=2x有两个交点时,其斜率k的取值范围是( )
A.(-2 ,2 ,2 ) ) | B.(- , , ) ) |
C.(-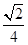 , ,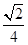 ) ) | D.(-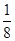 , ,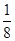 ) ) |
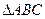 的三个顶点分别为
的三个顶点分别为 ,
,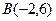 ,
,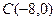
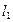 与直线
与直线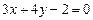 平行且与两坐标轴的正半轴围成的面积为12
平行且与两坐标轴的正半轴围成的面积为12  与直线
与直线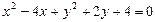 相切,求直线
相切,求直线