题目内容
设双曲线  ,离心率
,离心率  ,右焦点
,右焦点  ,方程
,方程  的两个实数根分别为
的两个实数根分别为  ,则点
,则点  与圆
与圆  的位置关系
的位置关系
| A.在圆内 | B.在圆上 | C.在圆外 | D.不确定 |
A
解析试题分析:由离心率  知,
知, =
=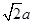 ,所以
,所以 =
= =
= ,所以
,所以 化为
化为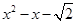 =0,
=0,
所以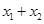 =1,
=1, =-
=-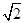 ,所以
,所以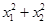 =
= =
=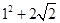 =
= <8,故点
<8,故点 在圆
在圆 内,故选A.
内,故选A.
考点:双曲线的性质,韦达定理,点与圆的位置关系

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知在平面直角坐标系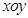 中,圆
中,圆 的方程为
的方程为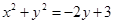 ,直线
,直线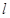 过点
过点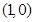 且与直线
且与直线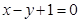 垂直.若直线
垂直.若直线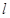 与圆
与圆 交于
交于 两点,则
两点,则 的面积为( )
的面积为( )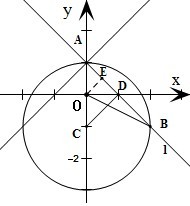
| A.1 | B.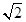 | C.2 | D.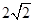 |
已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )
A.5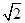 -4 -4 | B.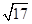 -1 -1 | C.6-2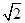 | D.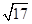 |
直线x-y+m=0与圆x2+y2-2x-1=0有两个不同的交点的一个充分不必要条件为( ).
| A.m<1 | B.-3<m<1 | C.-4<m<2 | D.0<m<1 |
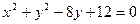 ,直线
,直线 :
: .
. 为何值时,直线
为何值时,直线 时,求
时,求 直线
直线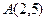 ,
,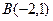 ,
,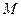 (在第一象限)和
(在第一象限)和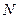 是过原点的直线
是过原点的直线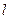 上的两个动点,且
上的两个动点,且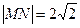 ,
,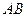 ,如果直线
,如果直线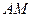 和
和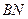 的交点
的交点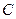 在
在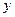 轴上,求点
轴上,求点