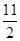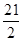题目内容
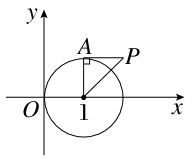
已知直线l过点(-2,0),当直线l与圆x2+y2=2x有两个交点时,其斜率k的取值范围是( )
A.(-2 ,2 ,2 ) ) | B.(- , , ) ) |
C.(-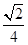 , ,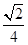 ) ) | D.(-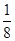 , ,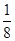 ) ) |
C
解析

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )
A.5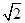 -4 -4 | B.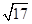 -1 -1 | C.6-2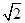 | D.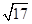 |
直线x-y+m=0与圆x2+y2-2x-1=0有两个不同的交点的一个充分不必要条件为( ).
| A.m<1 | B.-3<m<1 | C.-4<m<2 | D.0<m<1 |
过原点且倾斜角为 的直线被圆学
的直线被圆学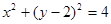 所截得的弦长为(科网 )
所截得的弦长为(科网 )
A.2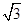 | B.2 | C.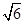 | D.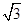 |
以抛物线y2=4x的焦点为圆心,且过坐标原点的圆的方程为( )
| A.x2+y2+2x=0 | B.x2+y2+x=0 |
| C.x2+y2﹣x=0 | D.x2+y2﹣2x=0 |