题目内容
18.若方程log2$\frac{{2}^{x}-1}{{2}^{x}+1}$=m在x∈[1,2]上有解,则实数m的取值范围为( )| A. | [1,2] | B. | [log2$\frac{1}{3}$,log2$\frac{3}{5}$] | C. | [-∞,log2$\frac{1}{3}$] | D. | [log2$\frac{3}{5}$,+∞] |
分析 由题意可得$\frac{{2}^{x}-1}{{2}^{x}+1}$=2m,再由$\frac{1}{3}$≤$\frac{{2}^{x}-1}{{2}^{x}+1}$≤$\frac{3}{5}$可得$\frac{1}{3}$≤2m≤$\frac{3}{5}$;从而解得.
解答 解:∵log2$\frac{{2}^{x}-1}{{2}^{x}+1}$=m,
∴$\frac{{2}^{x}-1}{{2}^{x}+1}$=2m,
又∵$\frac{{2}^{x}-1}{{2}^{x}+1}$=1-$\frac{2}{{2}^{x}+1}$,
又∵x∈[1,2],
∴$\frac{1}{3}$≤$\frac{{2}^{x}-1}{{2}^{x}+1}$≤$\frac{3}{5}$;
∴$\frac{1}{3}$≤2m≤$\frac{3}{5}$;
∴m∈[log2$\frac{1}{3}$,log2$\frac{3}{5}$],
故选B.
点评 本题考查了对数运算与指数运算的应用,属于基础题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
13.圆C1:(x-3)2+y2=1,圆C2:(x+3)2+y2=4,若圆M与两圆均外切,则圆心M的轨迹是( )
| A. | 双曲线的一支 | B. | 一条直线 | C. | 椭圆 | D. | 双曲线 |
8.已知向量$\overrightarrow{a}$=(x,1),$\overrightarrow{b}$=(-x,x2),则向量$\overrightarrow{a}$+$\overrightarrow{b}$( )
| A. | 与向量$\overrightarrow{c}$=(0,1)垂直 | B. | 与向量$\overrightarrow{c}$=(0,1)平行 | ||
| C. | 与向量$\overrightarrow{d}$=(1,-1)垂直 | D. | 与向量$\overrightarrow{d}$=(1,-1)平行 |
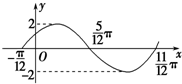 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$) 的部分图象如图所示.
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$) 的部分图象如图所示.