题目内容
13.已知定义在R上的函数f(x)的周期为4,且当x∈(-1,3]时,f(x)=$\left\{\begin{array}{l}{{x}^{2},x∈(-1,1]}\\{1+cos\frac{π}{2}x,x∈(1,3]}\end{array}\right.$,则函数g(x)=f(x)-log6x的零点个数是5.分析 函数g(x)=f(x)-log6x的零点个数可化为函数f(x)与函数y=log6x的图象的交点的个数,作函数图象求解.
解答 解:函数g(x)=f(x)-log6x的零点个数可化为
函数f(x)与函数y=log6x的图象的交点的个数,
由题意,作函数f(x)与函数y=log6x的图象如下,
结合函数图象可得,共有5个交点,
故答案为:5.
点评 本题考查了函数的零点与函数的图象的交点的关系应用及数形结合的思想应用,属于中档题.

练习册系列答案
相关题目
1.下列说法正确的是( )
| A. | 命题“若xy=0,则x=0或y=0”的否命题为“若xy≠0,则x≠0或y≠0” | |
| B. | 若命题p为假命题,命题¬q为真命题,则命题“p∨q”为真命题 | |
| C. | “$\frac{a}{b}$>1”是“a>b>0”的必要不充分条件 | |
| D. | 命题“任意x>1,x+1>2”的否定是“存在x≤1,x+1≤2” |
5. 已知可导函数y=f(x)在点P(x0,f(x0))处切线为l:y=g(x)(如图),设F(x)=f(x)-g(x),则( )
已知可导函数y=f(x)在点P(x0,f(x0))处切线为l:y=g(x)(如图),设F(x)=f(x)-g(x),则( )
 已知可导函数y=f(x)在点P(x0,f(x0))处切线为l:y=g(x)(如图),设F(x)=f(x)-g(x),则( )
已知可导函数y=f(x)在点P(x0,f(x0))处切线为l:y=g(x)(如图),设F(x)=f(x)-g(x),则( )| A. | F′(x0)=0,x=x0是F(x)的极大值点 | B. | F′(x0)=0,x=x0是F(x)的极小值点 | ||
| C. | F′(x0)≠0,x=x0不是F(x)的极值点 | D. | F′(x0)≠0,x=x0是F(x)的极值点 |
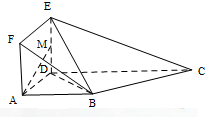 如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.
如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.