题目内容
设等差数列{an}的前n项和为Sn.已知a3=12,S12>0,S13<0.
(Ⅰ)求公差d的取值范围.
(Ⅱ)指出S1,S2,…,S12中哪一个值最大,并说明理由.
(Ⅰ)求公差d的取值范围.
(Ⅱ)指出S1,S2,…,S12中哪一个值最大,并说明理由.
本小题考查数列、不等式及综合运用有关知识解决问题的能力.
(Ⅰ)解:依题意,有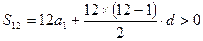
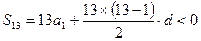 ,
,
即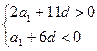 由a3=12,得a1=12-2d. ③
由a3=12,得a1=12-2d. ③
将③式分别代①、②式,得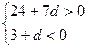 ,
,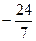 <d<-3
<d<-3
(Ⅱ)解法一:由d<0可知a1>a2>a3>…>a12>a13.
因此,若在1≤n≤12中存在自然数n,使得an>0,an+1<0,则Sn就是S1,S2,…,S12中的最大值.
由于 S12=6(a6+a7)>0,S13=13a7<0,即 a6+a7>0,a7<0,此得a6>-a7>0.
因为a6>0,a7<0,故在S1,S2,…,S12中S6的值最大.
(Ⅱ)解法二:
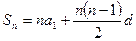
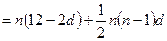
=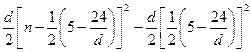 .
.
∵ d<0,∴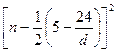 最小时,Sn最大.
最小时,Sn最大.
当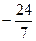 <d<-3时
<d<-3时 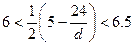 ,
,
∵正整数n=6时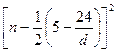 最小,∴S6最大.
最小,∴S6最大.
(Ⅲ)解法三:由d<0可知 a1>a2>a3>…>a12>a13.
因此,若在1≤n≤12中存在自然数n,使得an>0,an+1<0,
则Sn就是S1,S2,…,S12中的最大值.
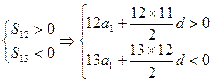
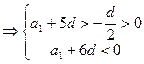
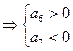
故在S1,S2,…,S12中S6的值最大.
(Ⅰ)解:依题意,有
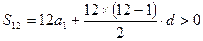
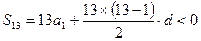 ,
,
|
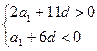 由a3=12,得a1=12-2d. ③
由a3=12,得a1=12-2d. ③将③式分别代①、②式,得
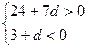 ,
,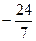 <d<-3
<d<-3(Ⅱ)解法一:由d<0可知a1>a2>a3>…>a12>a13.
因此,若在1≤n≤12中存在自然数n,使得an>0,an+1<0,则Sn就是S1,S2,…,S12中的最大值.
由于 S12=6(a6+a7)>0,S13=13a7<0,即 a6+a7>0,a7<0,此得a6>-a7>0.
因为a6>0,a7<0,故在S1,S2,…,S12中S6的值最大.
(Ⅱ)解法二:
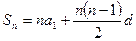
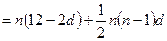
=
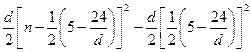 .
.∵ d<0,∴
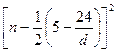 最小时,Sn最大.
最小时,Sn最大.当
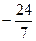 <d<-3时
<d<-3时 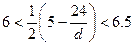 ,
,∵正整数n=6时
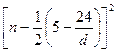 最小,∴S6最大.
最小,∴S6最大.(Ⅲ)解法三:由d<0可知 a1>a2>a3>…>a12>a13.
因此,若在1≤n≤12中存在自然数n,使得an>0,an+1<0,
则Sn就是S1,S2,…,S12中的最大值.
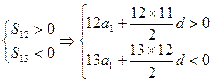
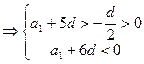
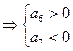
故在S1,S2,…,S12中S6的值最大.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 ,
,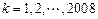 .证明:当且仅当
.证明:当且仅当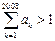 时,存在数列
时,存在数列 满足以下条件:
满足以下条件: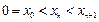 ,
, ;
;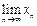 存在;
存在;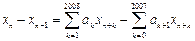 ,
,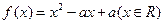 同时满足:①不等式
同时满足:①不等式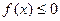 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在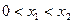 ,使得不等式
,使得不等式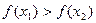 成立。设数列
成立。设数列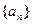 的前n项和
的前n项和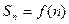 。(1)求
。(1)求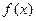 的解析式;(2)求数列
的解析式;(2)求数列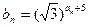 ,
,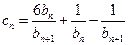 ,
,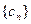 前n项和为
前n项和为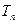 ,
,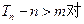 (
(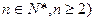 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.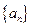 满足:
满足: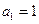 ,且对每个
,且对每个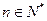 ,
,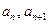 是方程
是方程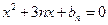 的两根,则
的两根,则 .
.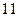
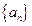 是等差数列,
是等差数列,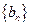 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且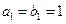 ,
,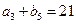 ,
,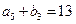 ;(1)求
;(1)求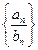 的前
的前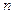 项和
项和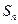 。
。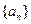 中,
中,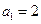 ,
,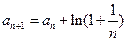 ,则
,则
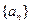 ,
,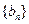 的前
的前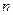 项和分别为
项和分别为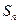 ,
,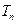 ,若
,若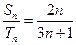 ,则
,则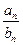 =( )
=( )
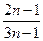
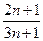
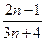
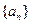 的前
的前 项和为
项和为 ,若
,若 ,
,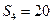 ,则
,则 ( )
( )