题目内容
设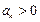 ,
,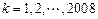 .证明:当且仅当
.证明:当且仅当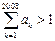 时,存在数列
时,存在数列 满足以下条件:
满足以下条件:
(ⅰ)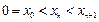 ,
, ;
;
(ⅱ)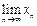 存在;
存在;
(ⅲ)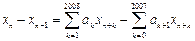 ,
, .
.
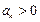 ,
,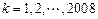 .证明:当且仅当
.证明:当且仅当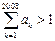 时,存在数列
时,存在数列 满足以下条件:
满足以下条件:(ⅰ)
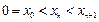 ,
, ;
;(ⅱ)
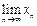 存在;
存在;(ⅲ)
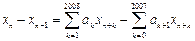 ,
, .
.[证] 必要性:假设存在 满足(ⅰ),(ⅱ),(iii).注意到(ⅲ)中式子可化为
满足(ⅰ),(ⅱ),(iii).注意到(ⅲ)中式子可化为
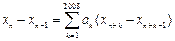 ,
,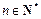 ,
,
其中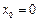 .
.
将上式从第1项加到第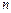 项,并注意到
项,并注意到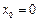 得
得
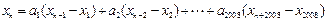 .
.
由(ⅱ)可设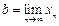 ,将上式取极限得
,将上式取极限得
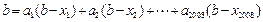
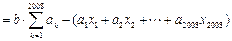
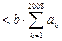 ,
,
因此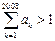 .
.
充分性:假设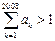 .定义多项式函数如下:
.定义多项式函数如下:
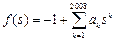 ,
,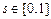 ,
,
则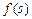 在[0,1]上是递增函数,且
在[0,1]上是递增函数,且
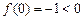 ,
,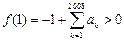 .
.
因此方程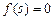 在[0,1]内有唯一的根
在[0,1]内有唯一的根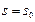 ,且
,且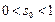 ,即
,即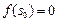 .
.
下取数列 为
为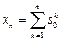 ,
,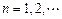 ,则明显地
,则明显地 满足题设条件(ⅰ),且
满足题设条件(ⅰ),且 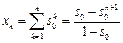 .
.
因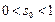 ,故
,故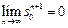 ,因此
,因此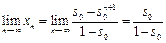 ,即
,即 的极限存在,满足(ⅱ).
的极限存在,满足(ⅱ).
最后验证 满足(ⅲ),因
满足(ⅲ),因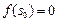 ,即
,即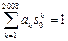 ,从而
,从而
 .
.
综上,已证得存在数列 满足(ⅰ),(ⅱ),(ⅲ).
满足(ⅰ),(ⅱ),(ⅲ).
 满足(ⅰ),(ⅱ),(iii).注意到(ⅲ)中式子可化为
满足(ⅰ),(ⅱ),(iii).注意到(ⅲ)中式子可化为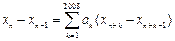 ,
,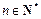 ,
,其中
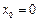 .
.将上式从第1项加到第
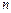 项,并注意到
项,并注意到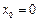 得
得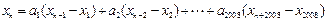 .
. 由(ⅱ)可设
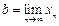 ,将上式取极限得
,将上式取极限得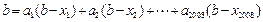
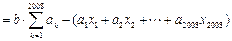
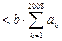 ,
,因此
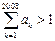 .
. 充分性:假设
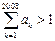 .定义多项式函数如下:
.定义多项式函数如下: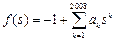 ,
,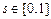 ,
,则
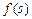 在[0,1]上是递增函数,且
在[0,1]上是递增函数,且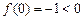 ,
,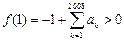 .
.因此方程
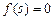 在[0,1]内有唯一的根
在[0,1]内有唯一的根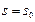 ,且
,且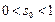 ,即
,即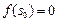 .
. 下取数列
 为
为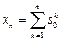 ,
,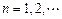 ,则明显地
,则明显地 满足题设条件(ⅰ),且
满足题设条件(ⅰ),且 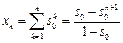 .
.因
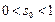 ,故
,故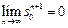 ,因此
,因此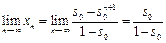 ,即
,即 的极限存在,满足(ⅱ).
的极限存在,满足(ⅱ). 最后验证
 满足(ⅲ),因
满足(ⅲ),因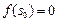 ,即
,即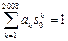 ,从而
,从而 .
.综上,已证得存在数列
 满足(ⅰ),(ⅱ),(ⅲ).
满足(ⅰ),(ⅱ),(ⅲ). 解析见答案

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
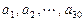 ,其中
,其中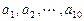 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;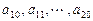 是公差为
是公差为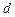 的等差数列;
的等差数列;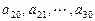 是公差为
是公差为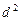 的等差数列(
的等差数列(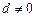 ).
).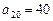 ,求
,求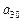 关于
关于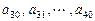 是公差为
是公差为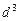 的等差数列,……,依次类推,把已知数列推广为无穷数列.提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列.提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?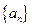 是等差数列,其中
是等差数列,其中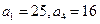
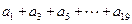 值。
值。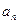 }中,
}中,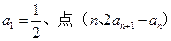 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….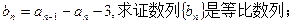 (Ⅱ)求数列
(Ⅱ)求数列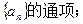
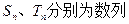
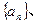
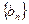 的前n项和,是否存在实数
的前n项和,是否存在实数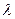 ,使得数列
,使得数列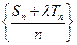 为等差数列?若存在,试求出
为等差数列?若存在,试求出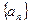 中,
中,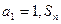 是数列
是数列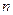 项和,对任意
项和,对任意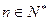 ,均有
,均有 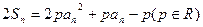 (1).求常数
(1).求常数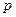 的值;(2)求数列
的值;(2)求数列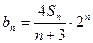 ,求数列
,求数列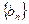 的前
的前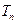 。
。 
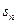 ,若
,若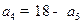 ,则
,则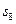 等于 ( )
等于 ( )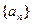 中,
中,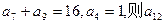 的值是( )
的值是( )