题目内容
15．已知数列{an}中，a1=1，an=an-1+$\frac{1}{n（n-1）}$（n≥2），则{an}的通项公式是2-$\frac{1}{n}$．分析 通过对an=an-1+$\frac{1}{n（n-1）}$（n≥2）变形、累加计算即得结论．
解答 解：∵an=an-1+$\frac{1}{n（n-1）}$（n≥2），
∴an-an-1=$\frac{1}{n（n-1）}$=$\frac{1}{n-1}$-$\frac{1}{n}$（n≥2），
an-1-an-2=$\frac{1}{n-2}$-$\frac{1}{n-1}$，
…
a2-a1=$\frac{1}{1}$-$\frac{1}{2}$，
累加得：an-a1=$\frac{1}{1}$-$\frac{1}{n}$，
又∵a1=1，
∴an=a1+$\frac{1}{1}$-$\frac{1}{n}$=2-$\frac{1}{n}$，
故答案为：2-$\frac{1}{n}$．
点评 本题考查数列的通项，注意解题方法的积累，属于中档题．
练习册系列答案
相关题目
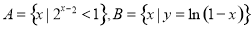，则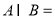
___________．