题目内容
6.从编号为1,2,…10的10个大小相同的球中任取4个,已知选出4号球的条件下,选出球的最大号码为6的概率为$\frac{1}{14}$.分析 令事件A={选出的4个球中含4号球},B={选出的4个球中最大号码为6},求出n(A)=C${\;}_{9}^{3}$=84,n(AB)=C${\;}_{4}^{2}$=6,即可求出选出4号球的条件下,选出球的最大号码为6的概率.
解答 解:令事件A={选出的4个球中含4号球},B={选出的4个球中最大号码为6}.
依题意知n(A)=C${\;}_{9}^{3}$=84,n(AB)=C${\;}_{4}^{2}$=6,
∴P(B|A)=$\frac{6}{84}$=$\frac{1}{14}$.
故答案为:$\frac{1}{14}$
点评 本题考查古典概型,理解古典概型的特征:试验结果的有限性和每一个试验结果出现的等可能性,掌握列举法,还要应用排列组合公式熟练,学会运用数形结合、分类讨论的思想解决概率的计算问题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
11.已知函数$f(x)=\frac{(sinx+cosx)-|sinx-cosx|}{2}$,则函数f(x)的值域为( )
| A. | [-1,1] | B. | [-1,$\frac{\sqrt{2}}{2}$] | C. | [-$\frac{\sqrt{2}}{2}$,1] | D. | [-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$] |
18.给出下面类比推理命题(其中Q为有理数集,R为实数集,C为复数集)
①“若a,b∈R,则a-b=0⇒a=b”类比推出“若a,b∈C,则a-b=0⇒a=b”
②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”
类比推出“若a,b,c,d∈Q,则a+b$\sqrt{2}$=c+d$\sqrt{2}$?a=c,b=d”;
其中类比结论正确的情况是( )
①“若a,b∈R,则a-b=0⇒a=b”类比推出“若a,b∈C,则a-b=0⇒a=b”
②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”
类比推出“若a,b,c,d∈Q,则a+b$\sqrt{2}$=c+d$\sqrt{2}$?a=c,b=d”;
其中类比结论正确的情况是( )
| A. | ①②全错 | B. | ①对②错 | C. | ①错②对 | D. | ①②全对 |
15.已知ξ的分布列如下:
并且η=3ξ+2,则方差Dη=( )
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{6}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{9}$ | D. | 5 |
15.已知函数f(x)=-x3+ax2-x-1在(-∞,+∞)上是单调函数,则实数a的取值范围是( )
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | (-$\sqrt{3}$,$\sqrt{3}$) | C. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | D. | (-∞,-$\sqrt{3}$)∩($\sqrt{3}$,+∞) |
 ,则
,则 的真子集可以是( )
的真子集可以是( ) B.
B. C.
C. D.
D.
 关于
关于 的方程
的方程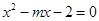 在
在 有解,命题
有解,命题 在
在 单调递增;若
单调递增;若 为真命题,
为真命题, 是真命题,求实数
是真命题,求实数 的取值范围.
的取值范围.