题目内容
10.求下列函数的值域:(1)y=x2+4x-2,x∈R;
(2)y=x2+4x-2,x∈[-5,0];
(3)y=x2+4x-2,x∈[-6,-3];
(4)y=x2+4x-2,x∈[0,2].
分析 根据二次函数的性质,先求出函数的单调性,从而分别求出区间是上的最值即可.
解答 解:y=x2+4x-2=(x+2)2-6,
(1)y≥-6,∴y=x2+4x-2,x∈R时的值域是:[-6,+∞);
(2)函数在[-5,-2)递减,在(-2,0]递增,
∴x=-2时,函数值最小,x=-5时,函数值最大,
∴函数的最小值是-6,最大值是3,
∴y=x2+4x-2,x∈[-5,0]的值域是:[-6,3];
(3)函数在[-6,-3]递减,
∴x=-6时,函数值最大,x=-3时,函数值最小,
∴最大值是10,最小值是-5;
∴y=x2+4x-2,x∈[-6,-3]的值域是:[-5,10];
(4)函数在[0,2]递增,
∴x=0时,函数值直最小,x=2时,函数值最大,
∴最大值是10,最小值是-2,
∴y=x2+4x-2,x∈[0,2]的值域是:[-2,10].
点评 本题考查了二次函数的性质,考查函数的单调性、最值问题,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知点F(c,0)分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点和上顶点,点B为直线l“x=$\frac{{a}^{2}}{c}$”上的一动点,且△ABF的外接圆面积最小值是4π,则当椭圆的短轴最长时,椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
18.给出下面类比推理命题(其中Q为有理数集,R为实数集,C为复数集)
①“若a,b∈R,则a-b=0⇒a=b”类比推出“若a,b∈C,则a-b=0⇒a=b”
②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”
类比推出“若a,b,c,d∈Q,则a+b$\sqrt{2}$=c+d$\sqrt{2}$?a=c,b=d”;
其中类比结论正确的情况是( )
①“若a,b∈R,则a-b=0⇒a=b”类比推出“若a,b∈C,则a-b=0⇒a=b”
②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”
类比推出“若a,b,c,d∈Q,则a+b$\sqrt{2}$=c+d$\sqrt{2}$?a=c,b=d”;
其中类比结论正确的情况是( )
| A. | ①②全错 | B. | ①对②错 | C. | ①错②对 | D. | ①②全对 |
18.设随机变量ξ服从正态分布N(0,1),P(ξ>1)=P,则P(-1<ξ<O)=( )
| A. | $\frac{1}{2}$P | B. | $\frac{1}{2}$-P | C. | 1-2P | D. | 1-P |
 函数
函数 在区间
在区间 上有1个零点;命题
上有1个零点;命题 函数
函数 与
与 轴交于不同的两点,如果
轴交于不同的两点,如果 是假命题,
是假命题, 是真命题,求
是真命题,求 的取值范围.
的取值范围. 关于
关于 的方程
的方程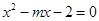 在
在 有解,命题
有解,命题 在
在 单调递增;若
单调递增;若 为真命题,
为真命题, 是真命题,求实数
是真命题,求实数 的取值范围.
的取值范围.