Question

【题目】某单位280名员工参加“我爱阅读”活动，他们的年龄在25岁至50岁之间，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示．
（I）现要从年龄低于40岁的员工中用分层抽样的方法抽取12人，则年龄在第1，2，3组的员工人数分别是多少？
（II）为了交流读书心得，现从上述12人中再随机抽取3人发言，设3人中年龄在[35，40）的人数为ξ，求ξ的数学期望；
（III）为了估计该单位员工的阅读倾向，现对从该单位所有员工中按性别比例抽取的40人做“是否喜欢阅读国学类书籍”进行调查，调查结果如下表所示：（单位：人）

	喜欢阅读国学类	不喜欢阅读国学类	合计
男	14	4	18
女	8	14	22
合计	22	18	40

根据表中数据，我们能否有99%的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系？
附： ，其中n=a+b+c+d

P（K2≥k0）	0.05	0.025	0.010	0.005	0.001
k0	3.841	5.024	6.635	7.879	10.828

Answer 1

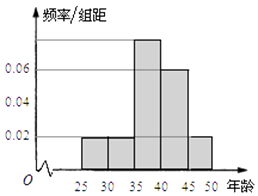
【答案】解：（Ⅰ）由频率分布直方图得前三组的人数分别为：0.02×5×280=28，28，

[1﹣（0.02+0.02+0.06+0.02）×5]×280=112

所以前三组抽取的人数分别为 ，2，8

（II）由上可知，ξ的所有可能取值为0，1，2，3，其概率分别为 ， ，

所以，

（Ⅲ）假设H0：“是否喜欢看国学类书籍和性别无关系”，根据表中数据，

求得K2的观测值 ，

查表得P（K2≥6.635）=0.01，从而能有99%的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系

【解析】（Ⅰ）由频率分布直方图得前三组的人数，即可求出年龄在第1，2，3组的员工人数分别是多少；（II）由上可知，ξ的所有可能取值为0，1，2，3，求出其概率，即可求ξ的数学期望；（III）求得K2的观测值，查表得P（K2≥6.635）=0.01，即可得出结论．
【考点精析】掌握频率分布直方图是解答本题的根本，需要知道频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息．