题目内容
已知单调递增的等比数列{an}满足:
a2+a3+a4=28,且a3+2是a2和a4的等差中项.
(1)求数列{an}的通项公式an;
(2)令bn=anlog an,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的最小的正整数n.
an,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的最小的正整数n.
a2+a3+a4=28,且a3+2是a2和a4的等差中项.
(1)求数列{an}的通项公式an;
(2)令bn=anlog
 an,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的最小的正整数n.
an,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的最小的正整数n.(1)2n(2)n=5.
(1)设{an}的公比为q,由已知,得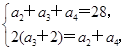 ∴
∴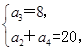
即 ,解得
,解得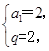 或
或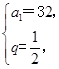 (舍去)∴an=a1qn-1=2n,
(舍去)∴an=a1qn-1=2n,
(2)bn=2nlog 2n=-n·2n,
2n=-n·2n,
设Tn=1×2+2×22+3×23+…+n×2n,①
则2Tn=1×22+2×23+…+(n-1)×2n+n×2n+1, ②
①-②得-Tn=(2+22+…+2n)-n×2n+1
=-(n-1)·2n+1-2,
∴Sn=-Tn=-(n-1)×2n+1-2,
由Sn+n·2n+1>50,得
-(n-1)·2n+1-2+n·2n+1>50,则2n>26,
故满足不等式的最小的正整数n=5.
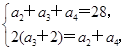 ∴
∴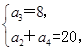
即
 ,解得
,解得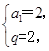 或
或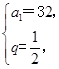 (舍去)∴an=a1qn-1=2n,
(舍去)∴an=a1qn-1=2n,(2)bn=2nlog
 2n=-n·2n,
2n=-n·2n,设Tn=1×2+2×22+3×23+…+n×2n,①
则2Tn=1×22+2×23+…+(n-1)×2n+n×2n+1, ②
①-②得-Tn=(2+22+…+2n)-n×2n+1
=-(n-1)·2n+1-2,
∴Sn=-Tn=-(n-1)×2n+1-2,
由Sn+n·2n+1>50,得
-(n-1)·2n+1-2+n·2n+1>50,则2n>26,
故满足不等式的最小的正整数n=5.

练习册系列答案
相关题目
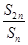 (n∈N*)是非零常数,则称该数列为“和等比数列”;若数列{cn}是首项为2,公差为d(d≠0)的等差数列,且数列{cn}是“和等比数列”,则d=________.
(n∈N*)是非零常数,则称该数列为“和等比数列”;若数列{cn}是首项为2,公差为d(d≠0)的等差数列,且数列{cn}是“和等比数列”,则d=________.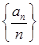 是递增数列;p4:数列{an+3nd}是递增数列.
是递增数列;p4:数列{an+3nd}是递增数列.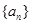 满足:当
满足:当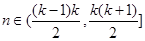 (
(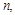
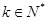 )时,
)时,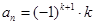 ,
,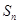 是数列
是数列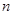 项和,定义集合
项和,定义集合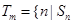 是
是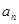 的整数倍,
的整数倍,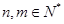 ,且
,且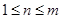
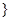 ,
,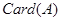 表示集合
表示集合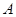 中元素的个数,则
中元素的个数,则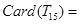 ,
,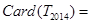 .
.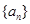 中,已知
中,已知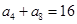 ,则该数列前11项的和
,则该数列前11项的和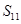 等于
等于