题目内容
设Sn为数列{an}的前n项和,若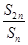 (n∈N*)是非零常数,则称该数列为“和等比数列”;若数列{cn}是首项为2,公差为d(d≠0)的等差数列,且数列{cn}是“和等比数列”,则d=________.
(n∈N*)是非零常数,则称该数列为“和等比数列”;若数列{cn}是首项为2,公差为d(d≠0)的等差数列,且数列{cn}是“和等比数列”,则d=________.
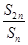 (n∈N*)是非零常数,则称该数列为“和等比数列”;若数列{cn}是首项为2,公差为d(d≠0)的等差数列,且数列{cn}是“和等比数列”,则d=________.
(n∈N*)是非零常数,则称该数列为“和等比数列”;若数列{cn}是首项为2,公差为d(d≠0)的等差数列,且数列{cn}是“和等比数列”,则d=________.4
由题意可知,数列{cn}的前n项和为Sn=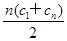 ,前2n项和为S2n=
,前2n项和为S2n=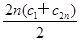 ,所以
,所以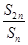 =
=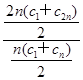 =2+
=2+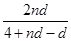 =2+
=2+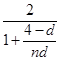 .因为数列{cn}是“和等比数列”,即
.因为数列{cn}是“和等比数列”,即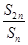 为非零常数,所以d=4.
为非零常数,所以d=4.
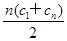 ,前2n项和为S2n=
,前2n项和为S2n=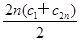 ,所以
,所以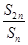 =
=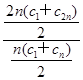 =2+
=2+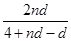 =2+
=2+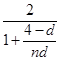 .因为数列{cn}是“和等比数列”,即
.因为数列{cn}是“和等比数列”,即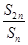 为非零常数,所以d=4.
为非零常数,所以d=4.
练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
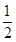 ,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.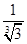 ,公比为
,公比为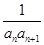 ,Tn为数列{bn}的前n项和.
,Tn为数列{bn}的前n项和.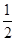 a11+6,则数列{an}前9项的和S9等于( ).
a11+6,则数列{an}前9项的和S9等于( ). an,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的最小的正整数n.
an,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的最小的正整数n.