题目内容
设{an}是公比大于1的等比数列,Sn为数列{an}的前n项和.已知S3=7,且a1+3,3a2,a3+4构成等差数列.
(1)求数列{an}的通项公式;
(2)令bn=ln a3n+1,n=1,2,…,求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)令bn=ln a3n+1,n=1,2,…,求数列{bn}的前n项和Tn.
(1)an=2n-1(2)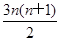 ln 2
ln 2
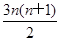 ln 2
ln 2(1)依题意,得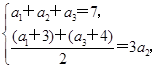
解得a2=2.
设等比数列{an}的公比为q,由a2=2,可得a1=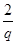 ,a3=2q.
,a3=2q.
又S3=7,可知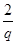 +2+2q=7,即2q2-5q+2=0,
+2+2q=7,即2q2-5q+2=0,
解得q=2或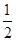 .
.
由题意,得q>1,∴q=2,∴a1=1.
故数列{an}的通项是an=2n-1.
(2)由于bn=ln a3n+1,n=1,2,…,
由(1)得a3n+1=23n,
∴bn=ln 23n=3n ln 2,
又bn+1-bn=3ln 2,
∴数列{bn}是等差数列.
∴Tn=b1+b2+…+bn=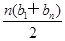 =
= ln 2.
ln 2.
故Tn=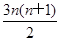 ln 2.
ln 2.
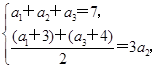
解得a2=2.
设等比数列{an}的公比为q,由a2=2,可得a1=
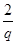 ,a3=2q.
,a3=2q.又S3=7,可知
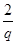 +2+2q=7,即2q2-5q+2=0,
+2+2q=7,即2q2-5q+2=0,解得q=2或
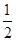 .
.由题意,得q>1,∴q=2,∴a1=1.
故数列{an}的通项是an=2n-1.
(2)由于bn=ln a3n+1,n=1,2,…,
由(1)得a3n+1=23n,
∴bn=ln 23n=3n ln 2,
又bn+1-bn=3ln 2,
∴数列{bn}是等差数列.
∴Tn=b1+b2+…+bn=
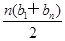 =
= ln 2.
ln 2. 故Tn=
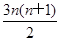 ln 2.
ln 2.
练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
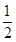 ,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.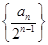 的前n项和.
的前n项和.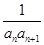 ,Tn为数列{bn}的前n项和.
,Tn为数列{bn}的前n项和.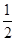 a11+6,则数列{an}前9项的和S9等于( ).
a11+6,则数列{an}前9项的和S9等于( ). an,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的最小的正整数n.
an,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的最小的正整数n.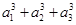 +…+
+…+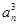 =
=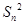 ,记Sn为数列{an}的前n项和.
,记Sn为数列{an}的前n项和.