Question

【题目】如图，在正三棱柱 ABC A1 B1C1 中， AB 3 ， AA1 4 ， M 为 AA1 的中点， P 是 BC 上一点，且由 P 沿棱柱侧面经过棱 CC1 到 M 点的最短路线长为 ，设这条最短路线与 CC1 的交点为 N 。求：

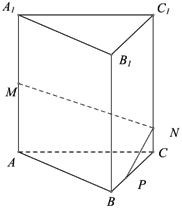
（1）该三棱柱的侧面展开图的对角线长；

（2） PC 和 NC 的长；

（3）平面 NMP 和平面 ABC 所成锐二面角大小的正切值.

Answer 1

【答案】（1） ；（2） PC 2 ， NC ；（3）

【解析】

（1）由展开图为矩形，用勾股定理求对角线长．

（2）在侧面展开图中三角形MAP1是直角三角形，可以求出线段AP的长度，进而可以求出PC的长度，再由相似比可以求得CN的长度．

（3）补形，找出两面的交线，在特殊的位置作出线面角，如图2．二面角易求．

解：（1）正三棱柱ABC﹣A1B1C1的侧面展开图是一个长为9，宽为4的矩形，其对角线长为

（2）如图1，将侧面BB1C1C绕棱CC1旋转120°使其与侧面AA1C1C在同一平面上，点P运动到点P1的位置，连接MP1，则MP1就是由点P沿棱柱侧面经过棱CC1到点M的最短路线

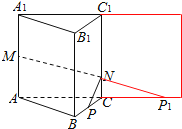
图1

设PC＝x，则P1C＝x，在Rt△MAP1中，由勾股定理得（3+x）2+22＝29

求得x＝2

∴PC＝P1C＝2

∵

∴

（3）如图2，连接PP1，则PP1就是平面NMP与平面ABC的交线，作NH⊥PP1于H，又CC1⊥平面ABC，连接CH，由三垂线定理得，CH⊥PP1

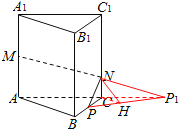
图2

∴∠NHC就是平面NMP与平面ABC所成二面角的平面角（锐角）

在Rt△PHC中，∵，∴

在Rt△NCH中，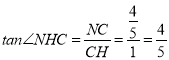

故平面 NMP 和平面 ABC 所成锐二面角大小的正切值为