题目内容
【题目】如果有穷数列
、
、
、
、
（
为正整数）满足条件
、
、
，即
，我们称其为“对称数列”.例如，数列
、
、
、、与数列
、
、、、、都是“对称数列”.
（1）设
是
项的“对称数列”，其中
、
、
、
是等差数列，且
，
，依次写出
的每一项；
（2）设
是
项的“对称数列”，其中
、
、、
是首项为，公比为的等比数列，求各项的和
；
（3）设
是
项的“对称数列”，其中
、
、、
是首项为，公差为
的等差数列，求前
项的和
.
【答案】（1）
、
、
、
、、、；（2）
；（3）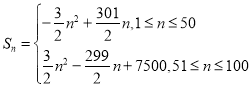
.
【解析】
（1）由
、
、
、
是等差数列，且
，
，先求出、、、，然后由“对称数列”的特点可写出数列
的各项；
（2）由
、
、
、
是首项为
，公比为的等比数列，先求出、、、的和，结合对称性数列对应项相等的特点，可知前面的各项，结合等比数列的求和公式可求出数列的和；
（3）由
、
、、
是首项为，公差为
的等差数列，可求出
、
、、
的通项，由对称数列的特点，可求出数列
前
项的和
.
（1）设数列、、、的公差为
，则
，解得
.
则
，
，因此，数列为：、、、、、、；
（2）由题意得
；
（3）
，
.
由题意可知，数列、、、
是首项为
，公差为
的等差数列.
当
时，
；
当
时，
.
因此，.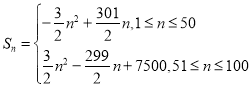
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】物价监督部门为调研某公司新开发上市的一种产品销售价格的合理性，对某公司的该产品的销量与价格进行了统计分析，得到如下数据和散点图：
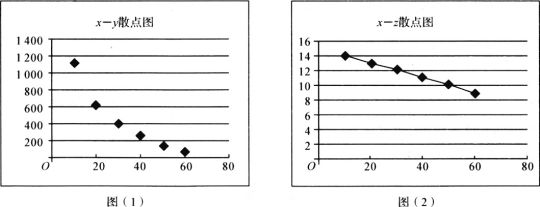
定价x（元／kg） | 10 | 20 | 30 | 40 | 50 | 60 |
年销量y（kg） | 1150 | 643 | 424 | 262 | 165 | 86 |
z＝21ny | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
（参考数据：
，
，
，
）
（Ⅰ）根据散点图判断，y与x和z与x哪一对具有的线性相关性较强（给出判断即可，不必说明理由）？
（Ⅱ）根据（Ⅰ）的判断结果及数据，建立y关于x的回归方程（方程中的系数均保留两位有效数字）．
附：对于一组数据（x1，y1），（x2，y2），（x3，y3），…，（xn，yn），其回归直线
的斜率和截距的最小二乘估计分别为
，
．
