题目内容
11.函数f (x)=$\left\{\begin{array}{l}2-|x|,x≤2\\{(x-2)^2},x>2\end{array}\right.$,若函y=f (x)十f(2-x)-b,b∈R恰4个零,则b的取值范围是( )| A. | ($\frac{7}{4}$,+∞) | B. | (一∞,$\frac{7}{4}$) | C. | (0,$\frac{7}{4}$) | D. | ($\frac{7}{4}$,2) |
分析 由题意得g(x)=f (x)十f(2-x)=$\left\{\begin{array}{l}{{x}^{2}+x+2,x<0}\\{2,0≤x≤2}\\{{x}^{2}-5x+8,x>2}\end{array}\right.$,作函数g(x)的图象,从而结合图象可求得.
解答 解:∵f (x)=$\left\{\begin{array}{l}2-|x|,x≤2\\{(x-2)^2},x>2\end{array}\right.$,
∴f(2-x)=$\left\{\begin{array}{l}{2-|2-x|,x≥0}\\{{x}^{2},x<0}\end{array}\right.$,
设g(x)=f (x)十f(2-x)
=$\left\{\begin{array}{l}{{x}^{2}+x+2,x<0}\\{2,0≤x≤2}\\{{x}^{2}-5x+8,x>2}\end{array}\right.$,
作函数g(x)的图象如下,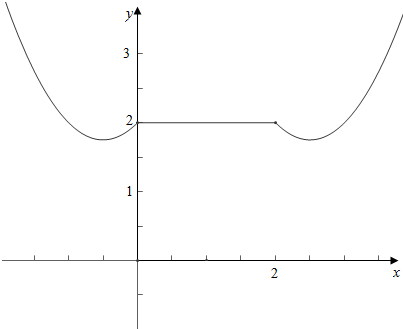 ,
,
g(-$\frac{1}{2}$)=$\frac{1}{4}$-$\frac{1}{2}$+2=$\frac{7}{4}$,g($\frac{5}{2}$)=$(\frac{5}{2})^{2}$-5×$\frac{5}{2}$+8=$\frac{7}{4}$;
结合图象可知,
b的取值范围是($\frac{7}{4}$,2);
故选:D.
点评 本题考查了函数的化简与分段函数的应用,同时考查了数形结合的思想应用.

练习册系列答案
相关题目
16.给出下列命题:
①若给定命题p:?x∈R,使得x2+x-1<0,则?p:?x∈R,均有x2+x-1≥0;
②若p∧q为假命题,则p,q均为假命题;
③命题“若x2-3x+2=0,则x=2”的否命题为“若 x2-3x+2=0,则x≠2,
其中正确的命题序号是( )
①若给定命题p:?x∈R,使得x2+x-1<0,则?p:?x∈R,均有x2+x-1≥0;
②若p∧q为假命题,则p,q均为假命题;
③命题“若x2-3x+2=0,则x=2”的否命题为“若 x2-3x+2=0,则x≠2,
其中正确的命题序号是( )
| A. | ① | B. | ①② | C. | ①③ | D. | ②③ |
1.已知函数$f(x)=sin(2x+ϕ)-\sqrt{3}cos(2x+ϕ)(0<ϕ<π)$是R上的偶函数,则ϕ的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |