题目内容
16．给出下列命题：①若给定命题p：?x∈R，使得x2+x-1＜0，则?p：?x∈R，均有x2+x-1≥0；
②若p∧q为假命题，则p，q均为假命题；
③命题“若x2-3x+2=0，则x=2”的否命题为“若 x2-3x+2=0，则x≠2，
其中正确的命题序号是（ ）
| A． | ① | B． | ①② | C． | ①③ | D． | ②③ |
分析 写出原命题的否定，可判断①；根据复合命题真假判断的真值表，可判断②；写出原命题的否命题，可判断③．
解答 解：若给定命题p：?x∈R，使得x2+x-1＜0，则?p：?x∈R，均有x2+x-1≥0，故①正确；
若p∧q为假命题，则p，q存在假命题，但不一定均为假命题，故②错误；
命题“若x2-3x+2=0，则x=2”的否命题为“若 x2-3x+2≠0，则x≠2”，故③错误；
故选：A
点评 本题以命题的真假判断为载体，考查了特称命题的否定，复合命题，四种命题，是简单逻辑的简单综合应用．
练习册系列答案
相关题目
7．直线$\sqrt{3}$x+y-1=0的倾斜角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
11．函数f （x）=$\left\{\begin{array}{l}2-|x|，x≤2\\{（x-2）^2}，x＞2\end{array}\right.$，若函y=f （x）十f（2-x）-b，b∈R恰4个零，则b的取值范围是（ ）
| A． | （$\frac{7}{4}$，+∞） | B． | （一∞，$\frac{7}{4}$） | C． | （0，$\frac{7}{4}$） | D． | （$\frac{7}{4}$，2） |
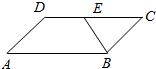如图，在平行四边形ABCD中，E是CD中点，$\overrightarrow{BE}=x\overrightarrow{AB}+y\overrightarrow{AD}$，则x+y=$\frac{1}{2}$．
8．函数g（x）=2x-a（x≤2）的值域为（ ）
| A． | （-∞，4-a] | B． | （0，4-a] | C． | [4-a，+∞） | D． | （-a，4-a] |