题目内容
1.已知函数$f(x)=sin(2x+ϕ)-\sqrt{3}cos(2x+ϕ)(0<ϕ<π)$是R上的偶函数,则ϕ的值为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 由条件利用两角和的正弦公式化简f(x)的解析式,再根据正弦函数、余弦函数的奇偶性,可得ϕ+$\frac{π}{3}$=kπ+$\frac{π}{6}$,求得ϕ的值.
解答 解:∵函数$f(x)=sin(2x+φ)-\sqrt{3}cos(2x+φ)$=2sin[(2x+ϕ)+$\frac{π}{3}$]=2sin(2x+ϕ+$\frac{π}{3}$)是R上的偶函数,
∴ϕ+$\frac{π}{3}$=kπ+$\frac{π}{2}$,求得ϕ=kπ+$\frac{π}{6}$,k∈Z,
故选:A.
点评 本题主要考查两角和的正弦公式,正弦函数、余弦函数的奇偶性,属于基础题.

练习册系列答案
相关题目
11.函数f (x)=$\left\{\begin{array}{l}2-|x|,x≤2\\{(x-2)^2},x>2\end{array}\right.$,若函y=f (x)十f(2-x)-b,b∈R恰4个零,则b的取值范围是( )
| A. | ($\frac{7}{4}$,+∞) | B. | (一∞,$\frac{7}{4}$) | C. | (0,$\frac{7}{4}$) | D. | ($\frac{7}{4}$,2) |
12.若关于x的不等式x2+|x+a|<2至少有一个正数解,则实数a的取值范围是( )
| A. | (-2,2) | B. | (-2,$\frac{9}{4}$) | C. | (-$\frac{9}{4}$,$\frac{9}{4}$) | D. | $(-\frac{9}{4},2)$ |
16.已知函数$f(x)=\root{3}{x}-{(\frac{1}{2})^x}$,那么在下列区间中含有函数f(x)零点的是( )
| A. | $(0,\frac{1}{3})$ | B. | $(\frac{1}{3},\frac{1}{2})$ | C. | $(\frac{1}{2},\frac{2}{3})$ | D. | $(\frac{2}{3},1)$ |
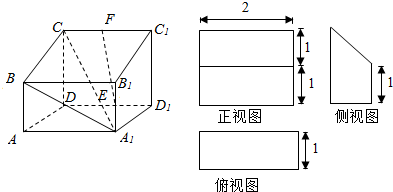 四棱柱ABCD-A1B1C1D1的三视图如图所示,E、F分别为A1B1、CC1的中点.
四棱柱ABCD-A1B1C1D1的三视图如图所示,E、F分别为A1B1、CC1的中点.