题目内容
9.若函数f(x)=-loga(x3+1)(a>0,a≠1)的定义域和值域都是[0,1],则a=( )| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 2 |
分析 根据对数函数的性质得到题中函数在[0,1]上是单调函数,结合f(0)=-loga1=0可得f(x)是增函数且f(1)=1.由此建立关于a的方程,解之即可得出实数a的值.
解答 解:根据对数函数的性质,可得函数f(x)=-loga(x3+1)在[0,1]上是单调函数,
∵函数f(x)=-loga(x3+1)满足f(0)=-loga1=0,
∴由函数的定义域和值域都是[0,1],
得函数f(x)是增函数且f(1)=1.
即-loga(1+1)=1,a=$\frac{1}{2}$,
故选:A.
点评 本题主要通过函数间的转化,来考查对数函数的定义域,值域及其单调性,还考查了转化和分类讨论思想.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
20.已知底面边长为$\sqrt{3}$的正三棱柱ABC-A1B1C1的体积为$\frac{9}{4}$,若点P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
1.已知向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(1,0),若(λ$\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,则实数λ的值为( )
| A. | -5 | B. | -$\frac{2}{5}$ | C. | -$\frac{3}{2}$ | D. | 5 |
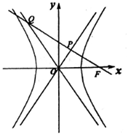 如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为2.
如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为2.