Question

【题目】（选修4﹣4：坐标系与参数方程）
已知直线l过点P（﹣1，2），且倾斜角为 ，圆方程为 ．
（1）求直线l的参数方程；
（2）设直线l与圆交与M、N两点，求|PM||PN|的值．

Answer 1

【答案】
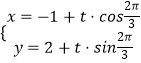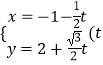（1）解：直线l过点P（﹣1，2），且倾斜角为 ，故直线l的参数方程为 ，即 为参数）
（2）解：圆方程 =2（ ﹣ ），即ρ2=2（ ﹣ ）=ρ cosθ﹣ ，

化为直角坐标方程为 + =1．

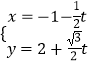把 代入 + =1化简可得 t2+（3+2 ）t+ =0．

设此一元二次方程式的两个根分别为 t1和 t2，则由根与系数的关系可得 t1t2= ．

由题意可得|PM||PN|=|t1||t2|=|t1t2|=

【解析】（1）由题意可得，直线l的参数方程为 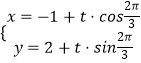，化简可得结果．（2）把圆的极坐标方程化为直角坐标方程可得 t2+（3+2 ）t+ =0，由根与系数的关系可得 t1t2= ，再由|PM||PN|=|t1||t2|=|t1t2|求得结果．
【考点精析】解答此题的关键在于理解直线的参数方程的相关知识，掌握经过点，倾斜角为的直线的参数方程可表示为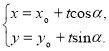（为参数）．