题目内容
已知数列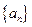 对任意的
对任意的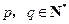 满足
满足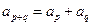 ,且
,且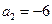 ,那么
,那么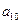 等于( )
等于( )
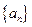 对任意的
对任意的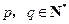 满足
满足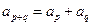 ,且
,且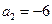 ,那么
,那么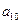 等于( )
等于( )A.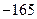 | B.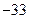 | C.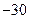 | D.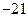 |
C
由已知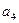 =
=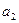 +
+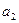 = -12,
= -12,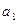 =
=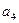 +
+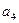 =-24,
=-24,
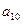 =
=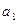 +
+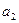 = -30
= -30
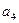 =
=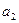 +
+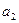 = -12,
= -12,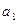 =
=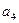 +
+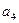 =-24,
=-24,
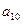 =
=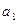 +
+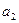 = -30
= -30
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
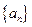 对任意的
对任意的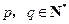 满足
满足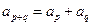 ,且
,且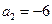 ,那么
,那么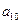 等于( )
等于( )A.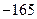 | B.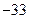 | C.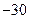 | D.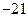 |
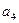 =
=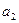 +
+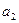 = -12,
= -12,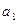 =
=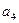 +
+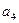 =-24,
=-24,
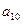 =
=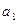 +
+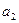 = -30
= -30
 阅读快车系列答案
阅读快车系列答案