题目内容
3.设函数$f(x)=\left\{{\begin{array}{l}{ln(-x){,_{\;}}x<0}\\{-lnx,{{,}_{\;}}x>0}\end{array}}\right.$若f(m)>f(-m),则实数m的取值范围是( )| A. | (-1,0)∪(0,1) | B. | .(-∞,-1)∪(0,1) | C. | (-1,0)∪(1,+∞) | D. | (-1,1] |
分析 由分段函数的解析式,讨论m>0,m<0,再由对数函数的单调性,解不等式,求并集即可得到.
解答 解:函数$f(x)=\left\{{\begin{array}{l}{ln(-x){,_{\;}}x<0}\\{-lnx,{{,}_{\;}}x>0}\end{array}}\right.$,
当m>0,f(m)>f(-m)即为-lnm>lnm,
即lnm<0,解得0<m<1;
当m<0,f(m)>f(-m)即为ln(-m)>-ln(-m),
即ln(-m)>0,解得m<-1.
综上可得,m<-1或0<m<1.
故选:B.
点评 本题考查分段函数的运用,考查对数函数的单调性的运用,运用分类讨论的思想方法是解题的关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
8.数列{an}中,an>0,a1=1,an+2=$\frac{1}{{{a_n}+1}}$,若a20=a16,则a2+a3=( )
| A. | $\frac{5}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{\sqrt{5}+1}}{2}$ |
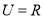 ,
,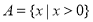 ,
,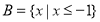 ,则集合
,则集合 ( )
( )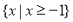 B.
B.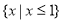
 D.
D.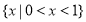
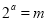 ,
, ,则
,则 等于( )
等于( ) B.
B.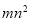
 D.
D.
 椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)在第一象限的部分与过点A(2,0)、B(0,1)的直线相切于点T,且椭圆的离心率e=$\frac{\sqrt{3}}{2}$.
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)在第一象限的部分与过点A(2,0)、B(0,1)的直线相切于点T,且椭圆的离心率e=$\frac{\sqrt{3}}{2}$.