题目内容
20.如图,F1,F2分别为椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,椭圆C上的点到F1点距离的最大值为5,离心率为$\frac{2}{3}$,A,B是椭圆C上位于x轴上方的两点,且直线AF1与直线BF2平行.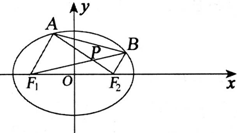
(Ⅰ)求椭圆C的方程;
(Ⅱ)若$\overrightarrow{A{F}_{1}}$=2$\overrightarrow{B{F}_{2}}$,求直线AF1的方程;
(Ⅲ)设AF2与BF1的交点为P,求证:|PF1|+|PF2|是定值.
分析 (Ⅰ)由题意知$\left\{\begin{array}{l}{a+c=5}\\{\frac{c}{a}=\frac{2}{3}}\end{array}\right.$,解可得a、c的值,从而可得b2的值,带入椭圆的标准方程可得答案;
(Ⅱ)根据题意,设A(x1,y1),B(x2,y2),延长AB,与x轴交与点M,分析可得M(6,0),进而设AB的直线方程为x+my-6=0,联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1}\\{x+my-6=0}\end{array}\right.$可得(9+5m2)y2-60my+135=0,由韦达定理,得$\left\{\begin{array}{l}{{y}_{1}+{y}_{2}=\frac{60m}{9+5{m}^{2}}}\\{{y}_{1}{y}_{2}=\frac{135}{9+5{m}^{2}}}\end{array}\right.$,又由$\overrightarrow{A{F}_{1}}$=2$\overrightarrow{B{F}_{2}}$,分析可得y1=2y2,联立两个式子解可得m的值,$\left\{\begin{array}{l}{{y}_{1}=\frac{5\sqrt{3}}{4}}\\{{y}_{2}=\frac{5\sqrt{3}}{8}}\end{array}\right.$,从而可得直线AF1的斜率,代入可得直线AF1的方程,
(Ⅲ)根据题意,由$\left\{\begin{array}{l}{x+2=ny}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1}\end{array}\right.$,可得(9+5n2)y2-20ny-25=0,解可得y1的值,进而可得|AF1|与|BF2|的值,进一步可以用n来表示|AF1|+|BF2|以及|AF1||BF2|,而|PF1|+|PF2|=6-$\frac{2|A{F}_{1}|B{F}_{2}||}{|A{F}_{1}|+|B{F}_{2}|}$,代入即可得到证明.
解答 解:(Ⅰ)由题意知$\left\{\begin{array}{l}{a+c=5}\\{\frac{c}{a}=\frac{2}{3}}\end{array}\right.$,得a=3,c=2;
从而b2=a2-c2=5;
所以椭圆C的方程为$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1.
(Ⅱ)由(Ⅰ)知:F1(-2,0),F2(2,0),设A(x1,y1),B(x2,y2),
延长AB,与x轴交与点M,由$\overrightarrow{A{F}_{1}}$=2$\overrightarrow{B{F}_{2}}$,可得BF2为△AF1M的中位线,所以|MF2|=|F1F2|,得M(6,0),
设AB的直线方程为x+my-6=0,(显然m>0)
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1}\\{x+my-6=0}\end{array}\right.$,消去x,整理可得(9+5m2)y2-60my+135=0,由韦达定理,得$\left\{\begin{array}{l}{{y}_{1}+{y}_{2}=\frac{60m}{9+5{m}^{2}}}\\{{y}_{1}{y}_{2}=\frac{135}{9+5{m}^{2}}}\end{array}\right.$,①
又由$\overrightarrow{A{F}_{1}}$=2$\overrightarrow{B{F}_{2}}$,得(-2-x1,-y1)=2(2-x2,-y2),所以y1=2y2,②
联立①②解可得m=$\frac{9\sqrt{3}}{5}$,$\left\{\begin{array}{l}{{y}_{1}=\frac{5\sqrt{3}}{4}}\\{{y}_{2}=\frac{5\sqrt{3}}{8}}\end{array}\right.$,从而x1=6-my1=-$\frac{3}{4}$,于是AF1的斜率K1=$\sqrt{3}$,直线AF1的方程为y=$\sqrt{3}$(x+2),
(Ⅲ)根据题意,直线AF1与直线BF2平行
设直线AF1的方程为x+2=ny,直线BF2的方程为x-2=ny,
由$\left\{\begin{array}{l}{x+2=ny}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1}\end{array}\right.$,可得(9+5n2)y2-20ny-25=0,
则y1=$\frac{10n+15\sqrt{{n}^{2}+1}}{9+5{n}^{2}}$,y2=$\frac{10n-15\sqrt{{n}^{2}+1}}{9+5{n}^{2}}$,(舍去)
所以|AF1|=$\sqrt{{n}^{2}+1}$×|0-y1|=$\frac{10n+15\sqrt{{n}^{2}+1}}{9+5{n}^{2}}$,
同理|BF2|=$\sqrt{{n}^{2}+1}$×|0-y2|=$\frac{-10n+15\sqrt{{n}^{2}+1}}{9+5{n}^{2}}$,
|AF1|+|BF2|=$\frac{30({n}^{2}+1)}{9+5{n}^{2}}$,
|AF1||BF2|=$\frac{25({n}^{2}+1)}{9+5{n}^{2}}$,
直线AF1与直线BF2平行,$\frac{|PB|}{|P{F}_{1}|}$=$\frac{|B{F}_{2}|}{|A{F}_{1}|}$,变形可得$\frac{|PB|+|P{F}_{1}|}{|P{F}_{1}|}$=$\frac{|B{F}_{1}|}{|P{F}_{1}|}$=$\frac{|B{F}_{1}|+|A{F}_{1}|}{|A{F}_{1}|}$,
即|PF1|=$\frac{|A{F}_{1}|}{|A{F}_{1}|+|B{F}_{2}|}$×|BF1|,
由点B在椭圆上知,BF1+BF2=6,∴|PF1|=$\frac{|A{F}_{1}|}{|A{F}_{1}|+|B{F}_{2}|}$×(6-|BF2|).
同理|PF2|=$\frac{|B{F}_{2}|}{|A{F}_{1}|+|B{F}_{2}|}$(6-|AF1|}.
因此|PF1|+|PF2|=6-$\frac{2|A{F}_{1}|B{F}_{2}||}{|A{F}_{1}|+|B{F}_{2}|}$=6-$\frac{\frac{50({n}^{2}+1)}{9+5{n}^{2}}}{\frac{30({n}^{2}+1)}{9+5{n}^{2}}}$=$\frac{13}{3}$,
故|PF1|+|PF2|是定值.
点评 本题考查椭圆与直线的综合运用,一般计算量较大,注意结合椭圆的基本性质,寻找解题的突破点.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案| A. | $\frac{5}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{\sqrt{5}+1}}{2}$ |
 ,设
,设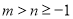 ,且
,且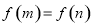 ,则
,则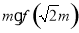 的最小值为( )
的最小值为( )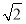 D.
D.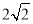
 椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)在第一象限的部分与过点A(2,0)、B(0,1)的直线相切于点T,且椭圆的离心率e=$\frac{\sqrt{3}}{2}$.
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)在第一象限的部分与过点A(2,0)、B(0,1)的直线相切于点T,且椭圆的离心率e=$\frac{\sqrt{3}}{2}$. 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=$\frac{1}{3}$BC
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=$\frac{1}{3}$BC