题目内容
已知函数 .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若函数 在
在 上无零点,求
上无零点,求 的最小值。
的最小值。
(1)  的单调递减区间为(0,2),单调递增区间为(2,
的单调递减区间为(0,2),单调递增区间为(2, ).
).
(2函数 在
在 上无零点,则
上无零点,则 的最小值为
的最小值为 .
.
解析试题分析:(1)当 时,
时, (
( ),则
),则 . 2分
. 2分
由 得
得 ;由
;由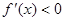 得
得 . 4分
. 4分
故 的单调递减区间为(0,2),单调递增区间为(2,
的单调递减区间为(0,2),单调递增区间为(2, ). 5分
). 5分
(2)要使函数 在
在 上无零点,只要对任意
上无零点,只要对任意 ,
, 无解.
无解.
即对 ,
, 无解. 7分
无解. 7分
令
 ,
, ,则
,则 , 9分
, 9分
再令 ,
, ,则
,则 . 11分
. 11分
故 在
在 为减函数,于是
为减函数,于是
 ,
,
从而 ,于是
,于是 在
在 上为增函数,
上为增函数,
所以 , 13分
, 13分
故要使 无解,只要
无解,只要 .
.
综上可知,若函数 在
在 上无零点,则
上无零点,则 的最小值为
的最小值为 . 14分
. 14分
考点:本题主要考查应用导数研究函数的单调性、最值及不等式证明问题,不等式的解法。
点评:难题,本题属于导数应用中的基本问题,通过研究函数的单调性,明确了极值情况。采用“表解法”,更加清晰明了。涉及函数零点的讨论问题,往往要转化成研究函数图象的大致形态,明确图象与x轴交点情况。本题涉及对数函数,要注意函数的定义域。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 取值范围.
取值范围. ,函数
,函数 ,
,  是函数
是函数 的极值点,求
的极值点,求 的值;
的值; 在区间
在区间 上的最值.
上的最值. 上为单调函数,若是,求出
上为单调函数,若是,求出
 的单调区间;
的单调区间; 上的最值.
上的最值. .
. 的单调性,并说明理由;
的单调性,并说明理由; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 在x=
在x= 与x =l时都取得极值
与x =l时都取得极值 在
在 时有极大值6,在
时有极大值6,在 时有极小值,求
时有极小值,求 的值;并求
的值;并求 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值. ,其中
,其中 .
. 恒成立,求
恒成立,求 的取值范围;
的取值范围; 的图像上取定两点
的图像上取定两点 ,记直线
,记直线 的斜率为
的斜率为 ,证明:存在
,证明:存在 ,使
,使 成立.
成立. .
. 处的切线方程;
处的切线方程; ,若在[1,e]上至少存在一点
,若在[1,e]上至少存在一点 ,使得
,使得 成立,求实数p的取值范围.
成立,求实数p的取值范围.