题目内容
17.为了了解某校学生对社会主义核心价值观的背诵掌握情况,拟采用分层抽样的方法从该校的高一、高二、高三这三个年级中共抽取7个班进行调查,已知该校的高一、高二、高三这三个年级分别有18、12、12个班级.(Ⅰ)求分别从高一、高二、高三这三个年级中抽取的班级个数;
(Ⅱ)若从抽取的7个班级中随机抽取2个班级进行调查结果的对比,求这2个班级中至少有1个班级来自高一年级的概率.
分析 (Ⅰ)由题意知总体个数是42,要抽取的个数是7,做出每个个体被抽到的概率,分别用三个年级的数目乘以概率,得到每一个年级要抽取的班数.
(Ⅱ)设A,B,C为在高一年级中抽取的3个班级,a,b为在高二年级中抽取的2个 班级1,2为在高三年级中抽取的2个班级,从这7个班级中随机抽取2个,全部的可能结果有21种,随机抽取的2个班级中至少有1个班级来自高一年级的结果有一共有15种,根据概率公式计算即可.
解答 解:(Ⅰ)班级总数为18+12+12=42,样本容量与总体中的个体数比为$\frac{7}{42}=\frac{1}{6}$,所以从高一、高二、高三这三个年级中分别抽取的班级个数为3,2,2.
(Ⅱ)设A,B,C为在高一年级中抽取的3个班级,a,b为在高二年级中抽取的2个 班级1,2为在高三年级中抽取的2个班级,从这7个班级中随机抽取2个,全部的可能结果有21种,分别如下,AB,AC,Aa,Ab,A1,A2,BC,Ba,Bb,B1,B2,Ca,Cb,C1,C2,ab,a1,a2,b1,b2,12,
随机抽取的2个班级中至少有1个班级来自高一年级的结果有一共有15种AB,AC,Aa,Ab,A1,A2,BC,Ba,Bb,B1,B2,Ca,Cb,C1,C2.
所以概率为$P=\frac{15}{21}=\frac{5}{7}$,
答:这2个班级中至少有1个班级来自高一年级的概率为$\frac{5}{7}$.
点评 本题主要考查分层抽样的定义和方法,以及古典概率的问题,属于基础题.

练习册系列答案
相关题目
12.某次数学测试后从两个班中各随机的抽取10名学生的数学成绩,作出它们的茎叶图如图所示,已知甲班的中位数为a1,标准差为s1,乙班的中位数为a2,标准差为s2,则由茎叶图可得( )
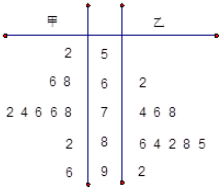

| A. | a1<a2,s1>s2 | B. | a1<a2,s1<s2 | C. | a1>a2,s1>s2 | D. | a1>a2,s1<s2 |
2.已知函数f(x)=log4[(4x+1)4kx](k∈R)为偶函数.
(1)求k的值;
(2)设g(x)=log4(a•2x+1),若函数f(x)与g(x)图象有且只有一个公共点,求实数a的取值范围.
(1)求k的值;
(2)设g(x)=log4(a•2x+1),若函数f(x)与g(x)图象有且只有一个公共点,求实数a的取值范围.
7.实数x,y满足(1+i)x+(1-i)y=2,则|x+yi|=( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |