��Ŀ����
8����1��ij�����ӹ�ij��������������ּӹ������ӹ��;��ӹ���ÿ���������ʱ����Ҫ�Բ�Ʒ���м��飮�ּӹ��ĺϸ�Ʒ���뾫�ӹ������ϸ���뷵�ӹ������ӹ��ĺϸ�Ʒ���뾫�ӹ������ϸ�Ʒ��Ϊ��Ʒ���������ӹ��ĺϸ�ƷΪ��Ʒ�����ϸ�ƷΪ��Ʒ��������ͼ��ʾ�������ļӹ����̣�
��2�����һ���ṹͼ����ʾ����ѧѡ��1-2���ڶ��¡�������֤������֪ʶ�ṹ��
���� ��1�����չ����Ҫ�����ù��������ͼ���ɣ�
��2�����ݡ���ѧѡ��1-2���ڶ��¡�������֤������֪ʶ������֪ʶ�ṹͼ��
��� �⣺��1�����չ���Ҫ��������Ĺ�������ͼ���£�
��2�����һ���ṹͼ����ʾ����ѧѡ��1-2���ڶ��¡�������֤������֪ʶ�ṹ���£�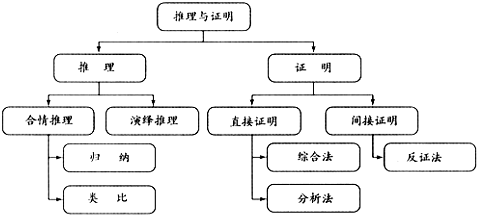
���� ���⿼���˸��ݹ�������ͼ�Լ�����֪ʶ���ݻ�֪ʶ�ṹͼ��Ӧ�����⣬�ǻ�����Ŀ��

��ϰ��ϵ�д�
 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�
�����Ŀ
3����֪����f��x��=$\left\{\begin{array}{l}2{x^3}+3{x^2}+m��0��x��1\\ mx+5��x��1.\end{array}$������f��x����ͼ����x������ֻ��������ͬ�Ľ��㣬��ʵ��m��ȡֵ��Χ�ǣ�������
| A�� | ��-1��-2�� | B�� | ��-2��-3�� | C�� | ��-2��-4�� | D�� | ��-5��0�� |
19����֪����$f��x��=\frac{{{2^x}-{2^{-x}}}}{2}��g��x��=\frac{{{2^x}+{2^{-x}}}}{2}$�����н��۴�����ǣ�������
| A�� | ����f��x����ͼ�����ԭ��Գƣ�����g��x����ͼ�����y��Գ� | |
| B�� | ��ͬһ����ϵ�У�����f��x����ͼ���ں���g��x����ͼ����·� | |
| C�� | ����g��x����ֵ����[1��+�ޣ� | |
| D�� | g��2x��=2f��x��g��x���ڣ�-�ޣ�+�ޣ������ |