题目内容
如图,在三棱锥S ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
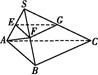
求证:(1)平面EFG∥平面ABC;
(2)BC⊥SA.
 ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.
求证:(1)平面EFG∥平面ABC;
(2)BC⊥SA.
(1)见解析 (2)见解析
证明:(1)因为AS=AB,AF⊥SB,垂足为F,
所以F是SB的中点.
又因为E是SA的中点,
所以EF∥AB.
因为EF?平面ABC,AB?平面ABC,
所以EF∥平面ABC.
同理EG∥平面ABC.
又EF∩EG=E,
所以平面EFG∥平面ABC.
(2)因为平面SAB⊥平面SBC,且交线为SB,
又AF?平面SAB,AF⊥SB,
所以AF⊥平面SBC.
因为BC?平面SBC,
所以AF⊥BC.
又因为AB⊥BC,AF∩AB=A,AF?平面SAB,
AB?平面SAB,
所以BC⊥平面SAB.
因为SA?平面SAB,
所以BC⊥SA.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
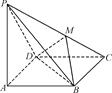
 ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
 ;若不存在,说明理由.
;若不存在,说明理由. 外一点可以作无数条直线与平面
外一点可以作无数条直线与平面 垂直平面
垂直平面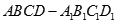 中,
中,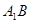 与平面
与平面 所成的角的大小是
所成的角的大小是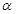 ,下列命题正确的是( )
,下列命题正确的是( ) 则
则
 则
则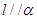
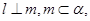 则
则
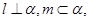 则
则
 a
a α;
α;