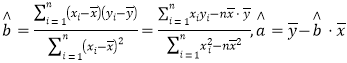��Ŀ����
����Ŀ��ij��������һ��������Ԫ�������������������ͼ���ˮƽ�����ƣ������һЩ��Ʒ�����ݾ���֪�������Ʒ��![]() ���ղ���
���ղ���![]() �������֮�������ϵ��
�������֮�������ϵ��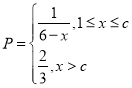 ��
��![]() ����֪ÿ����1����ϸ����������ӯ��2��Ԫ����ÿ����1�����Ʒ������1��Ԫ���ʳ���ϣ���������ʵ��ղ���.��ע����Ʒ��=��Ʒ��/��������
����֪ÿ����1����ϸ����������ӯ��2��Ԫ����ÿ����1�����Ʒ������1��Ԫ���ʳ���ϣ���������ʵ��ղ���.��ע����Ʒ��=��Ʒ��/��������
��1���Խ�������������Ԫ��ÿ���ӯ����![]() ����Ԫ����ʾΪ�ղ���
����Ԫ����ʾΪ�ղ���![]() ��������ĺ�����
������������
��2�����ղ���Ϊ����ʱ���ɻ���������
���𰸡���1��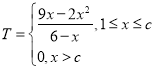 ��2��3���
��2��3���
��������
��1��ÿ���Ӯ��ΪT���ղ�����x������Ʒ�ʣ�1��P����2���ղ�����x������Ʒ�ʣ�P����1�����ݷֶκ����ֶ��о����������ɣ�
��2�����û�������ʽ�����������ֵ��
��1����x��cʱ��P![]() ��
��
��T![]() x2
x2![]() x1��0
x1��0
��1��x��cʱ��![]() ��
��
��![]()
���ϣ���ӯ����T����Ԫ�����ղ���x��������ĺ�����ϵΪ��
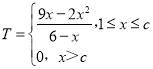
��2���ɣ�1��֪����x��cʱ��ÿ���ӯ����Ϊ0
��1��x��c����3��c��6����ʱ��T![]() 15��2[��6��x��
15��2[��6��x��![]() ]��15��12��3
]��15��12��3
���ҽ���x��3ʱȡ�Ⱥ�
��Tmax��3����ʱx��3
���Ե��ղ���Ϊ3���ʱ���ɻ���������.

����Ŀ��������һֱ����в���ǵ����ij������������Ϊ���о������в�����ֳ����![]() ��������ʱ��
��������ʱ��![]() ���죩�仯�Ĺ��ɣ��ռ��������£�
���죩�仯�Ĺ��ɣ��ռ��������£�
���� | 1 | 2 | 3 | 4 | 5 | 6 |
��ֳ���� | 6 | 12 | 25 | 49 | 95 | 190 |
����ɢ��ͼ�ɿ���������ֲ���һ��ָ���ͺ���![]() ����Χ.
����Χ.
����С�������λ���IJο����ݣ�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]()
��1�����![]() ����
����![]() �Ļع鷽�̣�����С�������λ���֣���
�Ļع鷽�̣�����С�������λ���֣���
��2����֪![]() �����������IJв�.
�����������IJв�.
�ο���ʽ��