题目内容
19.已知函数f(x)=$\frac{ax}{{x}^{2}+b}$,且f(x)的图象在x=1处与直线y=2相切.(1)求函数f(x)的解析式;
(2)若P(x0,y0)为f(x)图象上的任意一点,直线l与f(x)的图象切于P点,求直线l的斜率k的取值范围.
分析 (1)由求导公式和法则求出f′(x),根据题意和导数的几何意义列出方程组,求出a、b的值即可求出f(x);
(2)由(1)求出f′(x),由导数的几何意义得直线l的斜率k=f′(x0),利用分离常数法化简,利用换元法和二次函数的性质求出k的最小值和最大值,可得k的取值范围.
解答 解:(1)由题意得,f′(x)=$\frac{(ax)′({x}^{2}+b)-ax({x}^{2}+b)′}{{(x}^{2}+b)^{2}}$
=$\frac{a({x}^{2}+b)-2a{x}^{2}}{{{(x}^{2}+b)}^{2}}$=$\frac{-a{x}^{2}+ab}{{{(x}^{2}+b)}^{2}}$,
因为f(x)的图象在x=1处与直线y=2相切,
所以$\left\{\begin{array}{l}{f′(1)=\frac{-a+ab}{{(1+b)}^{2}}=0}\\{f(1)=\frac{a}{1+b}=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=4}\\{b=1}\end{array}\right.$,
则$f(x)=\frac{4x}{{x}^{2}+1}$;
(2)由(1)可得,f′(x)=$\frac{-4{x}^{2}+4}{{{(x}^{2}+1)}^{2}}$,
所以直线l的斜率k=f′(x0)=$\frac{-4{{x}_{0}}^{2}+4}{{{({x}_{0}}^{2}+1)}^{2}}$=$\frac{-4({{x}_{0}}^{2}+1)+8}{{{({x}_{0}}^{2}+1)}^{2}}$
=-4•$\frac{1}{{{x}_{0}}^{2}+1}$+$\frac{8}{{{({x}_{0}}^{2}+1)}^{2}}$,
设t=$\frac{1}{{{x}_{0}}^{2}+1}$,则t∈(0,1],
所以k=4(2t2-t)=8(t-$\frac{1}{4}$)2-$\frac{1}{2}$,
则在对称轴t=$\frac{1}{4}$处取到最小值$-\frac{1}{2}$,在t=1处取到最大值4,
所以直线l的斜率k的取值范围是[$-\frac{1}{2}$,4].
点评 本题考查导数的几何意义,求导公式和法则,以及二次函数的性质,考查分离常数法、换元法的应用,属于中档题.

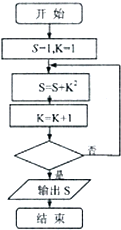
| A. | K<4 | B. | K<5 | C. | K<6 | D. | K<7 |
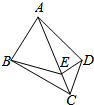 如图,空间四边形ABCD,∠CAD=45°,cos∠ACB=$\frac{\sqrt{15}}{5}$,AC=$\sqrt{15}$+$\sqrt{10}$,AD=2$\sqrt{5}$,BC=6,若点E在线段AC上运动,则EB+ED的最小值为7.
如图,空间四边形ABCD,∠CAD=45°,cos∠ACB=$\frac{\sqrt{15}}{5}$,AC=$\sqrt{15}$+$\sqrt{10}$,AD=2$\sqrt{5}$,BC=6,若点E在线段AC上运动,则EB+ED的最小值为7.