题目内容
2.已知函数f(x)对x∈R,都有f(x+2)=f(x),当0≤x≤2时,f(x)=x(2-x).设g(x)=$\left\{\begin{array}{l}{f(x)\\;x≥0}\\{\frac{1}{50}x+1\\;x<0}\end{array}\right.$,则g(x)的图象中关于y轴对称的点共有( )| A. | 96对 | B. | 100对 | C. | 48对 | D. | 50对 |
分析 根据函数的周期性和对称性求出当x>0,图象关于y轴对称的函数,结合函数的周期性进行求解即可
解答 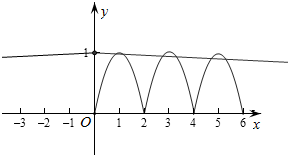 解:由f(x+2)=f(x),得函数的周期为2,
解:由f(x+2)=f(x),得函数的周期为2,
∵当x<0时,g(x)=$\frac{1}{50}$x+1,
∴若x>0时,-x<0,则g(-x)=-$\frac{1}{50}$x+1,
若函数g(x)关于y轴对称,
则g(x)=g(-x)=-$\frac{1}{50}$x+1,
作出对应的图象如图,
当x>0时,由g(x)=-$\frac{1}{50}$x+1=0得x=50,
即有25个周期,每个周期两个函数图象有2个交点,
则g(x)的图象中关于y轴对称的点共有50对.
故选:D.
点评 本题主要考查函数图象的交点个数的判断,利用偶函数的对称性以及函数的周期性是解决本题的关键.

练习册系列答案
相关题目
13.已知回归直线方程中斜率的估计值为1.23,样本点的中心(5,6.2),则回归直线方程为( )
| A. | y=1.23x-0.05 | B. | y=1.23x+0.05 | C. | y=1.23x+6.2 | D. | y=1.23x+5 |
10.某程序框图如图所示,若其输出结果是56,则判断框中应填写的是( )
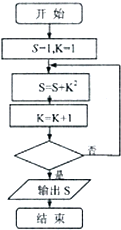

| A. | K<4 | B. | K<5 | C. | K<6 | D. | K<7 |
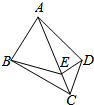 如图,空间四边形ABCD,∠CAD=45°,cos∠ACB=$\frac{\sqrt{15}}{5}$,AC=$\sqrt{15}$+$\sqrt{10}$,AD=2$\sqrt{5}$,BC=6,若点E在线段AC上运动,则EB+ED的最小值为7.
如图,空间四边形ABCD,∠CAD=45°,cos∠ACB=$\frac{\sqrt{15}}{5}$,AC=$\sqrt{15}$+$\sqrt{10}$,AD=2$\sqrt{5}$,BC=6,若点E在线段AC上运动,则EB+ED的最小值为7.