题目内容
1.若椭圆的焦点在y轴上,长轴长为4,离心率e=$\frac{\sqrt{3}}{2}$,则其标准方程为${x}^{2}+\frac{{y}^{2}}{4}=1$.分析 根据已知结合椭圆的性质,分别求出a,b,c的值,可得椭圆的方程.
解答 解:∵长轴长2a=4,
∴a=2,
∵离心率e=$\frac{\sqrt{3}}{2}$,
∴c=$\sqrt{3}$,
∴b2=a2-c2=1,
又∵椭圆的焦点在y轴上,
故椭圆的标准方程为:${x}^{2}+\frac{{y}^{2}}{4}=1$,
故答案为:${x}^{2}+\frac{{y}^{2}}{4}=1$
点评 本题考查的知识点是椭圆的标准方程,难度不大,属于基础题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
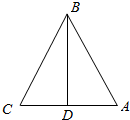 如图所示,△ABC中,AC=10cm,AC边上的高BD=10cm,求其水平放置的直观图的面积.
如图所示,△ABC中,AC=10cm,AC边上的高BD=10cm,求其水平放置的直观图的面积.