题目内容
9.已知O为坐标原点,点A的坐标是(2,3),点P(x,y)在不等式组$\left\{\begin{array}{l}{x+y≥3}\\{2x+y≤6}\\{x+2y≤6}\end{array}\right.$所确定的平面区域内(包括边界)运动,则$\overrightarrow{OA}•\overrightarrow{OP}$的取值范围是( )| A. | [4,10] | B. | [6,9] | C. | [6,10] | D. | [9,10] |
分析 设z=$\overrightarrow{OA}•\overrightarrow{OP}$,则z=2x+3y,作出不等式组对应的平面区域,利用线性规划的知识进行求解即可.
解答 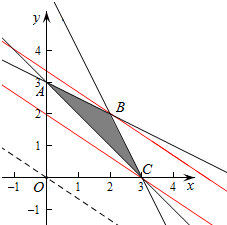 解:设z=$\overrightarrow{OA}•\overrightarrow{OP}$,则z=2x+3y,
解:设z=$\overrightarrow{OA}•\overrightarrow{OP}$,则z=2x+3y,
作出不等式组对应的平面区域如图:
由z=2x+3y得y=-$\frac{2}{3}$x+$\frac{1}{3}$z,
平移直线y=-$\frac{2}{3}$x+$\frac{1}{3}$z,由图象可知当直线y=-$\frac{2}{3}$x+$\frac{1}{3}$z经过点C(3,0)时,
直线y=-$\frac{2}{3}$x+$\frac{1}{3}$z的截距最小,此时z最小,此时zmin=2×3=6,
直线y=-$\frac{2}{3}$x+$\frac{1}{3}$z经过点B时,
直线y=-$\frac{2}{3}$x+$\frac{1}{3}$z的截距最小,此时z最小,
由$\left\{\begin{array}{l}{2x+y=6}\\{x+2y=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,即B(2,2),此时zmax=2×2+3×2=10,
故6≤z≤10
故选:C.
点评 本题主要考查线性规划的应用,根据向量的数量积,以及数形结合是解决本题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
20.若f(n)=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2n+1}$(n∈N*),则当n=2时,f(n)是( )
| A. | 1+$\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | 1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$ | D. | 非以上答案 |
17.“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(Ⅰ)若某参与者接受挑战后,对其他3个人发出邀请,则这3个人中恰有2个人接受挑战的概率是多少?
(Ⅱ)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下2×2列联表:
根据表中数据,是否有99%的把握认为“冰桶挑战赛与受邀者的性别有关”?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
(Ⅰ)若某参与者接受挑战后,对其他3个人发出邀请,则这3个人中恰有2个人接受挑战的概率是多少?
(Ⅱ)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下2×2列联表:
| 接受挑战 | 不接受挑战 | 合计 | |
| 男性 | 50 | 10 | 60 |
| 女性 | 25 | 15 | 40 |
| 合计 | 75 | 25 | 100 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
4.对于R上可导的任意函数f(x),若满足(x-2)f′(x)≥0,则必有( )
| A. | f(0)+f(3)<2f(2) | B. | f(0)+f(3)≤2f(2) | C. | f(0)+f(3)≥2f(2) | D. | f(0)+f(3)>2f(2) |
18.圆:x2+y2-4x+6y=0的圆心坐标和半径分别为( )
| A. | (-2,3),13 | B. | (-2,3),$\sqrt{13}$ | C. | (2,-3),$\sqrt{13}$ | D. | (2,-3),13 |