题目内容
设Sn为等比数列{an}的前n项和,若
=6,则
=______.
| S8 |
| S4 |
| S12 |
| S8 |
在等比数列{an}中,设S4=k,
由
=6,则S8=6k.
∵S4,S8-S4,S12-S8构成等比数列,
∴k,5k,S12-6k构成等比数列,
即25k2=k(S12-6k),解得:S12=31k.
∴
=
=
.
故答案为:
.
由
| S8 |
| S4 |
∵S4,S8-S4,S12-S8构成等比数列,
∴k,5k,S12-6k构成等比数列,
即25k2=k(S12-6k),解得:S12=31k.
∴
| S12 |
| S8 |
| 31k |
| 6k |
| 31 |
| 6 |
故答案为:
| 31 |
| 6 |

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
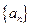 的前
的前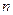 项和为
项和为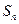 ,且
,且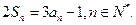
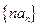 的前
的前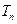 .
.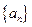 中,已知
中,已知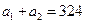 ,
,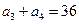 ,则
,则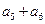 =
=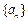 的各项为正,公比
的各项为正,公比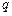 满足
满足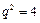 ,则
,则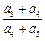 的值为()
的值为()
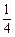
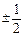
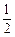
 是公比为正数的等比数列,若
是公比为正数的等比数列,若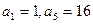 ,则数列
,则数列