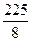题目内容
数列{an}中,若a1=1,an+1=2an+1,(n∈N*),那么an=______.
∵an+1=2an+1,∴an+1+1=2(an+1),
∵a1=1,∴a1+1=2≠0,
∴数列{an+1}是以2为首项,2为公比的等比数列,
∴an+1=2n,
∴an=2n-1.
故答案为:2n-1.
∵a1=1,∴a1+1=2≠0,
∴数列{an+1}是以2为首项,2为公比的等比数列,
∴an+1=2n,
∴an=2n-1.
故答案为:2n-1.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
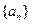 的公比为正数,且
的公比为正数,且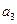 ·
·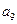 =2
=2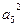 ,
,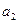 =1,则
=1,则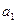 = ( )
= ( )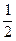
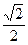
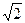
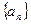 中,如果
中,如果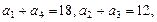 那么该数列的前
那么该数列的前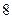 项之和为( )
项之和为( )