题目内容
已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上截距相等,求切线的方程;
(2)从圆C外一点P(x,y)向圆引切线PM,M为切点,O为坐标原点,且有|PM|=|PO|,求使|PM|最小的点P的坐标.
(1)若圆C的切线在x轴和y轴上截距相等,求切线的方程;
(2)从圆C外一点P(x,y)向圆引切线PM,M为切点,O为坐标原点,且有|PM|=|PO|,求使|PM|最小的点P的坐标.
1、切线方程为y=(2±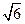 )x,x+y+1=0或x+y-3=0.
)x,x+y+1=0或x+y-3=0.
2、P(-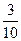 ,
,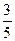 ).
).
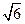 )x,x+y+1=0或x+y-3=0.
)x,x+y+1=0或x+y-3=0.2、P(-
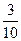 ,
,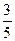 ).
).(1)圆C:x2+y2+2x-4y+3=0的标准方程为(x+1)2+(y-2)2=2,
∴圆心C(-1,2),半径r=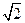 .
.
设圆C的切线在x轴和y轴上的截距分别为a、b.
当a=b=0时,
切线方程可设为y=kx,
即kx-y=0.
由点到直线的距离公式得
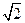 =
=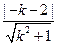 .解得k=2±
.解得k=2±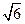 .
.
∴切线方程为y=(2±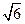 )x.
)x.
当a=b≠0时,
切线方程为 +
+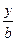 =1,
=1,
即x+y-a=0.
由点到直线的距离公式得
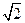 =
=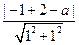 .
.
解之,得a=-1或a=3.
∴切线方程为x+y+1=0,x+y-3=0.
总之,所求切线方程为y=(2±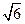 )x,x+y+1=0或x+y-3=0.
)x,x+y+1=0或x+y-3=0.
(2)连结MC,则|PM|2=|PC|2-|MC|2.
∵|PM|=|PO|,
∴|PC|2-|MC|2=|PO|2,
即(x+1)2+(y-2)2-2=x2+y2.
整理得x=2y-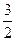 .
.
∴|PM|=|PO|=
=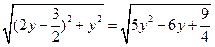 .
.
当y=-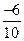 =
=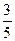 时,|PM|最小,
时,|PM|最小,
此时x=2×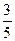 -
-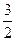 =-
=-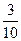 .
.
∴P(-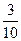 ,
,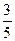 ).
).
∴圆心C(-1,2),半径r=
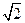 .
.设圆C的切线在x轴和y轴上的截距分别为a、b.
当a=b=0时,
切线方程可设为y=kx,
即kx-y=0.
由点到直线的距离公式得
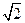 =
=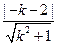 .解得k=2±
.解得k=2±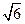 .
.∴切线方程为y=(2±
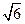 )x.
)x.当a=b≠0时,
切线方程为
 +
+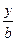 =1,
=1,即x+y-a=0.
由点到直线的距离公式得
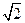 =
=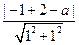 .
.解之,得a=-1或a=3.
∴切线方程为x+y+1=0,x+y-3=0.
总之,所求切线方程为y=(2±
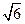 )x,x+y+1=0或x+y-3=0.
)x,x+y+1=0或x+y-3=0.(2)连结MC,则|PM|2=|PC|2-|MC|2.
∵|PM|=|PO|,
∴|PC|2-|MC|2=|PO|2,
即(x+1)2+(y-2)2-2=x2+y2.
整理得x=2y-
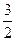 .
.∴|PM|=|PO|=

=
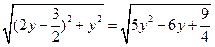 .
.当y=-
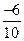 =
=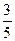 时,|PM|最小,
时,|PM|最小,此时x=2×
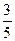 -
-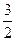 =-
=-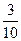 .
.∴P(-
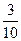 ,
,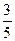 ).
).
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
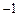 和3,在y轴上的一个截距为1.
和3,在y轴上的一个截距为1.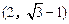 的直线l被圆C截得的弦AB的长为4,求直线l的倾斜角.
的直线l被圆C截得的弦AB的长为4,求直线l的倾斜角.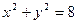
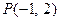
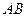
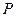
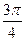 时,求弦
时,求弦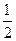 =0与圆(x-cosβ)2+(y+sinβ)2=
=0与圆(x-cosβ)2+(y+sinβ)2=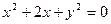 的圆心C,且与直线x+y=0垂直的直线方程是( )
的圆心C,且与直线x+y=0垂直的直线方程是( )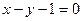
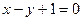
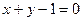
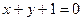
 内一点
内一点 ,过点
,过点 的直线
的直线 的倾斜角为
的倾斜角为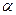 ,直线
,直线 ,
, .(1)当
.(1)当 时,求
时,求 的长;(2)当弦
的长;(2)当弦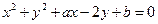 上,点P关于直线
上,点P关于直线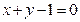 的对称点也在圆C上,则圆C的半径为 .
的对称点也在圆C上,则圆C的半径为 .