题目内容
已知向量a=(2cosα,2sinα),b=(3cosβ,3sinβ),a与b的夹角为60°,则直线xcosα-ysinα+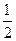 =0与圆(x-cosβ)2+(y+sinβ)2=
=0与圆(x-cosβ)2+(y+sinβ)2=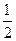 的位置关系是( )
的位置关系是( )
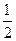 =0与圆(x-cosβ)2+(y+sinβ)2=
=0与圆(x-cosβ)2+(y+sinβ)2=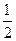 的位置关系是( )
的位置关系是( )| A.相切 | B.相交 |
| C.相离 | D.随α、β的值而定 |
C
∵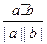 =cos60°=
=cos60°=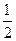 ,
,
∴cosαcosβ+sinαsinβ=cos(α-β)=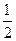 .
.
而圆心到直线的距离d=|cosαcosβ+sinαsinβ+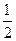 |=|cos(α-β)+
|=|cos(α-β)+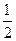 |=1大于圆的半径,故直线与圆相离.
|=1大于圆的半径,故直线与圆相离.
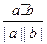 =cos60°=
=cos60°=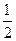 ,
,∴cosαcosβ+sinαsinβ=cos(α-β)=
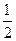 .
.而圆心到直线的距离d=|cosαcosβ+sinαsinβ+
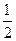 |=|cos(α-β)+
|=|cos(α-β)+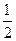 |=1大于圆的半径,故直线与圆相离.
|=1大于圆的半径,故直线与圆相离.
练习册系列答案
相关题目
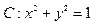 ,点
,点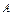 (-2,0)及点
(-2,0)及点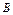 (2,
(2,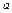 ),从
),从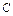 挡住,则
挡住,则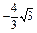 )∪(
)∪(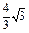 ,+∞) D.(-∞,-4)∪(4,+∞)
,+∞) D.(-∞,-4)∪(4,+∞) 在极坐标系中的方程为
在极坐标系中的方程为 ,圆C在极坐标系中的方程为
,圆C在极坐标系中的方程为 ,求圆C被直线
,求圆C被直线 、
、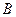 为椭圆
为椭圆 的左右顶点,
的左右顶点,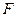 为椭圆的右焦点,
为椭圆的右焦点, 是椭圆上异于
是椭圆上异于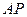 、
、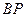 分别交直线
分别交直线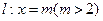 于
于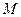 、
、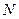 两点,
两点,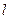 交
交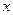 轴于
轴于 点.
点. 时,求直线
时,求直线 的方程;
的方程;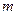 ,使得以
,使得以 为直径的圆过点
为直径的圆过点