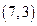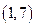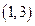题目内容
在直角坐标平面上,O为原点,M为动点,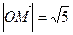 ,
,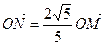 .过点M作MM1⊥
.过点M作MM1⊥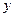 轴于M1,过N作NN1⊥
轴于M1,过N作NN1⊥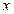 轴于点N1,
轴于点N1,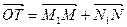 .记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线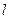 交曲线C于两个不同的点P、Q(点Q在A与P之间).
交曲线C于两个不同的点P、Q(点Q在A与P之间).
(Ⅰ)求曲线C的方程;
(Ⅱ)证明不存在直线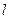 ,使得
,使得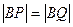 ;
;
(Ⅲ)过点P作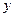 轴的平行线与曲线C的另一交点为S,若
轴的平行线与曲线C的另一交点为S,若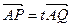 ,证明
,证明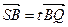 .
.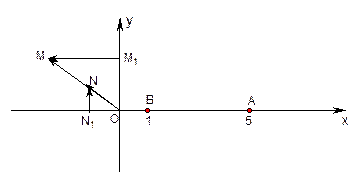
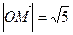 ,
,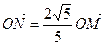 .过点M作MM1⊥
.过点M作MM1⊥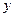 轴于M1,过N作NN1⊥
轴于M1,过N作NN1⊥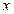 轴于点N1,
轴于点N1,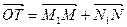 .记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线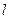 交曲线C于两个不同的点P、Q(点Q在A与P之间).
交曲线C于两个不同的点P、Q(点Q在A与P之间).(Ⅰ)求曲线C的方程;
(Ⅱ)证明不存在直线
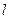 ,使得
,使得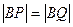 ;
;(Ⅲ)过点P作
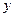 轴的平行线与曲线C的另一交点为S,若
轴的平行线与曲线C的另一交点为S,若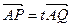 ,证明
,证明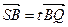 .
.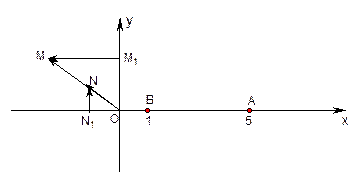
(Ⅰ)曲线C的方程: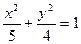 (2)同解析 (3)同解析
(2)同解析 (3)同解析
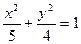 (2)同解析 (3)同解析
(2)同解析 (3)同解析 (1)解:设点T的坐标为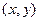 ,点M的坐标为
,点M的坐标为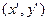 ,则M1的坐标为
,则M1的坐标为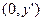
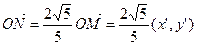 ∴点N的坐标为
∴点N的坐标为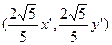
∴N1的坐标为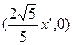 ∴
∴
由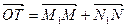 有
有 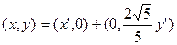
∴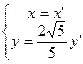 由此得
由此得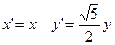
由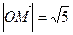 有
有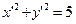
∴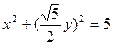 即
即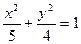 ,即为所求的方程.曲线C为椭圆.
,即为所求的方程.曲线C为椭圆.
(2)证:点A(5,0)在曲线C即椭圆的外部,当直线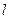 的斜率不存在时,直线
的斜率不存在时,直线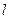 与椭圆C无交点,所以直线
与椭圆C无交点,所以直线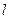 斜率存在,并设为
斜率存在,并设为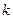 .直线
.直线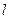 的方程为
的方程为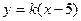 .
.
由方程组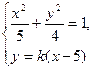 得
得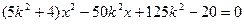
依题意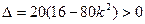 ,得
,得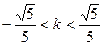 .
.
当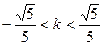 时,设交点
时,设交点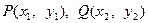 ,PQ的中点为R
,PQ的中点为R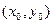 ,则
,则
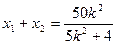 ,
, 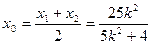
∴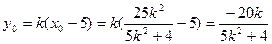
又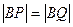
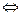 BR⊥
BR⊥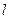
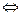
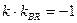
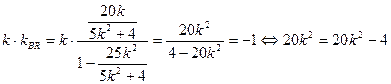
但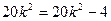 不可能成立,所以不存在直线
不可能成立,所以不存在直线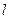 使得
使得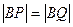 .
.
(3)证明:由题有S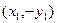 ,
,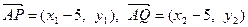 .
.
则有方程组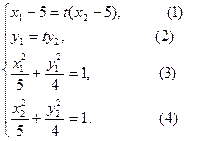
由(1)得: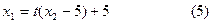
将(2)、(5)代入(3)有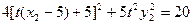
整理并将(4)、(5)代入得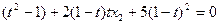
易知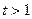 ,解得
,解得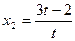
因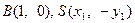 ,故
,故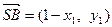 ,
,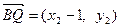 ,
,
∴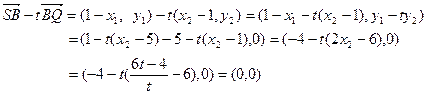
∴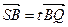 .
.
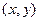 ,点M的坐标为
,点M的坐标为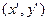 ,则M1的坐标为
,则M1的坐标为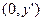
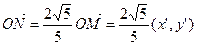 ∴点N的坐标为
∴点N的坐标为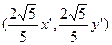
∴N1的坐标为
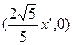 ∴
∴
由
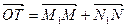 有
有 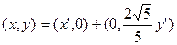
∴
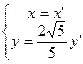 由此得
由此得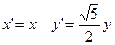
由
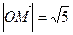 有
有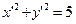
∴
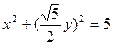 即
即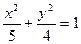 ,即为所求的方程.曲线C为椭圆.
,即为所求的方程.曲线C为椭圆. (2)证:点A(5,0)在曲线C即椭圆的外部,当直线
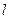 的斜率不存在时,直线
的斜率不存在时,直线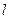 与椭圆C无交点,所以直线
与椭圆C无交点,所以直线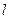 斜率存在,并设为
斜率存在,并设为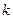 .直线
.直线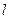 的方程为
的方程为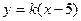 .
. 由方程组
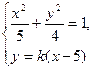 得
得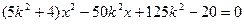
依题意
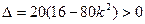 ,得
,得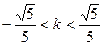 .
. 当
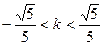 时,设交点
时,设交点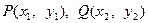 ,PQ的中点为R
,PQ的中点为R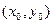 ,则
,则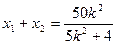 ,
, 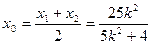
∴
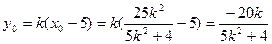
又
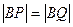
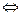 BR⊥
BR⊥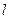
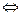
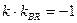
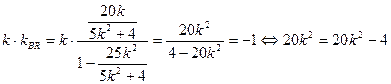
但
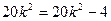 不可能成立,所以不存在直线
不可能成立,所以不存在直线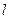 使得
使得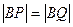 .
. (3)证明:由题有S
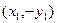 ,
,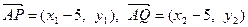 .
.则有方程组
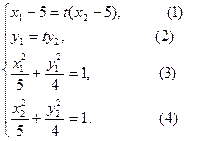
由(1)得:
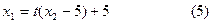
将(2)、(5)代入(3)有
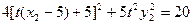
整理并将(4)、(5)代入得
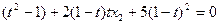
易知
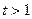 ,解得
,解得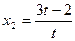
因
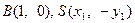 ,故
,故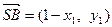 ,
,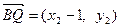 ,
,∴
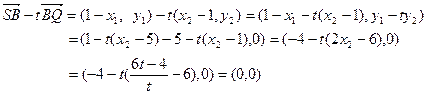
∴
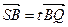 .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
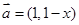 ,
,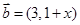 ,则“
,则“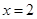 ”是“
”是“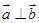 ”的
”的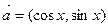
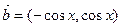
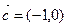
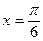 ,求向量
,求向量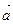 、
、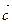 的夹角;
的夹角;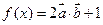 的单调递减区间
的单调递减区间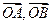 满足
满足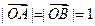 ,
,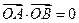 ,
,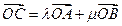
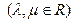 若
若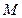 为
为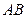 的中点,并且
的中点,并且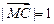 ,则点
,则点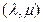 在( )
在( )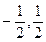 )为圆心,半径为1的圆上
)为圆心,半径为1的圆上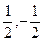 )为圆心,半径为1的圆上
)为圆心,半径为1的圆上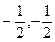 )为圆心,半径为1的圆上
)为圆心,半径为1的圆上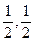 )为圆心,半径为1的圆上
)为圆心,半径为1的圆上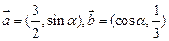 且
且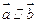 ,则锐角
,则锐角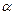 等于 ( )
等于 ( ) 
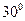

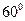
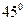
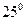
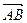 与
与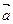 =(2,3)同向,
=(2,3)同向,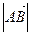 =2
=2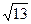 ,则点B的坐标为 .
,则点B的坐标为 .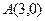 、
、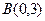 、
、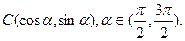
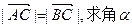 的值; (2)若
的值; (2)若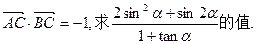
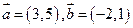 ,则
,则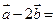 ( )
( )